人工智能已在众多领域展现了卓越的应用潜力，但AI模型的训练往往需要耗费大量时间和计算资源，背后也蕴含着复杂的优化理论和动力学问题。模型的训练（即目标函数的优化）问题通常面临两个主要挑战：一是高维非凸优化问题带来的复杂损失景观；二是大规模数据和深层网络的计算代价。在本项工作中，研究团队融合数值优化、动力系统、控制理论、数值计算等多个方向，为理解深度学习的训练机制带来新的研究视角。

当前，多数深度学习模型的训练最终可归结为高维优化问题求解，而基于梯度的方法是求解优化问题的关键，如SGD、Adam、重球法等常用方法。如何理解这些优化算法的本质及其动态过程，是突破深度学习可解释性的一大挑战。团队通过引入虚拟物理学来建模优化过程（如当前工作运用了经典力学二阶ODE建模），随后把优化问题转化成高维参数空间中的动力学控制问题，如此一来，丰富的反馈控制理论体系可以为优化算法设计与收敛性分析提供全新的思路。 

针对如何加速训练神经网络这一问题，该工作将控制科学中使用最为广泛的比例-积分-微分（PID）反馈控制律应用于刻画优化过程的虚拟物理动力学，创新地提出用于深度学习的连续时间PID加速优化器（Proportional-Integral-Derivative Accelerated Optimization, PIDAO）。通过构建合适的Lyapunov函数来建立PIDAO中超参数与稳定性之间的关系，以及动力系统平衡点与高维参数空间训练问题最优性的关联。 

相比于Polyak提出的重球法，PIDAO不再单一受梯度调控其优化方向，而是通过PID反馈给寻优机器人以函数梯度（当前“地势”）、一段历史梯度积分（过往“地势”）以及前方梯度趋势（未来“地势”）三类信息，来控制导航寻优过程。简单来说，Polyak方法用到了“现在”，Nesterov方法用到了“现在”和“未来”，而PIDAO融合三类信息共同决策寻优。 

用于深度学习的PID加速优化算法的基本思想

此外，基于Lyapunov稳定性理论，研究团队提供了PIDAO在凸优化问题和非凸优化问题的超参数选取范围，同时发现PIDAO优化器的抵消效应，该特性使得PIDAO具有更强的探索损失景观的能力。此外，借助 PID 控制器和 PIDAO 之间的联系，研究团队提供了PIDAO优化器的超参数可解释性。利用不同离散化方法对PIDAO离散化，进而发展出用于神经网络训练的PIDAO优化器并集成于深度学习框架（如Pytorch）。与基准优化算法方法（如Adam）相比，PIDAO系列算法在不同的测试场景中均获得更高的训练精度和更快的收敛速度。 

该项研究所提出的受控重球优化器框架和加速优化算法PIDAO，有助于加速深度学习模型训练，同时也为基于控制理论方法研究深度学习问题提供了新思路。

近年来，浙江大学控制科学与工程学院研究团队重点关注控制科学与机器学习的交叉研究，特别是 Control for Learning（控制赋能学习），这属于 Science for AI 范畴，近期相关的工作包括：分布式优化求解（Liu et al., IET CSR, 2023）、基于鲁棒控制的神经网络设计（Chen et al., IEEE TNNLS）、基于反馈的神经网络模型设计（Wang et al., Neurocomputing, 2024）等。此外，团队在 AI for Science 方面发表了大规模粒子智能可视计算（Liang et al., Nature Machine Intelligence）等工作。

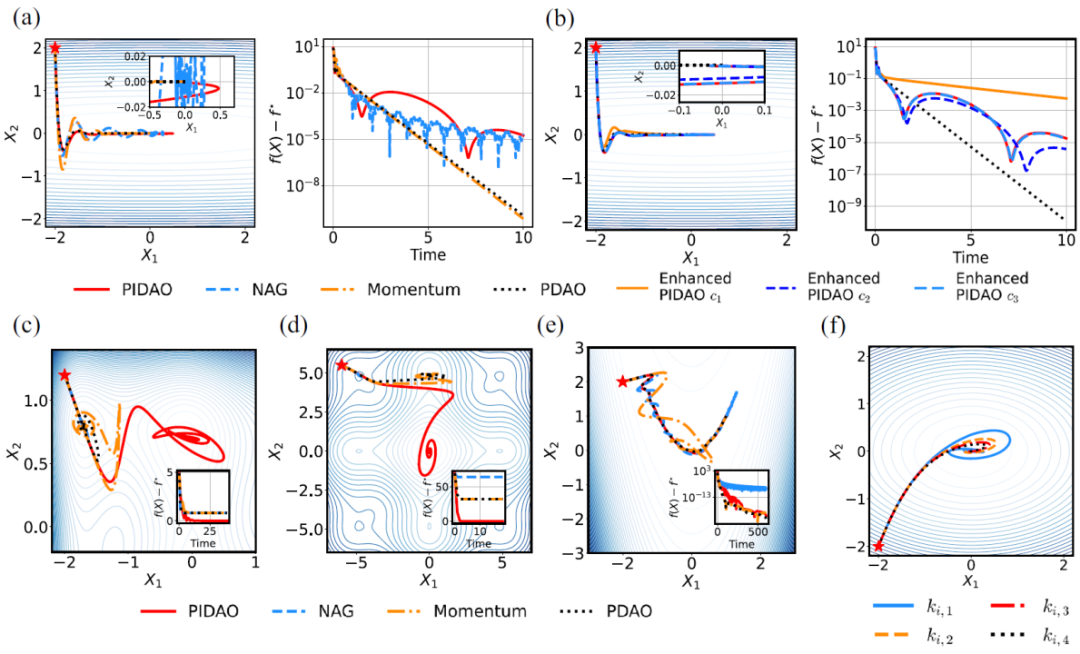
经典算法与PIDAO算法，在凸优化与非凸优化问题的对比

 PIDAO与Adam等经典算法在神经网络，求解偏微分方程问题上的性能对比