导语

今天我们将带大家来学习一个基本的概念，就是幂律分布。这部分的知识来自于集智百科，集智百科是复杂系统领域的百科全书，涵盖复杂系统领域的基本概念。（目前正在不断的完善阶段）

我们正在组织撰写翻译相应的维基词条，并附上代码实现。想要自己创建词条，一起贡献知识的小伙伴们可以通过链接报名哦。点击「编辑」，做些改变，按下「保存」，你将影响世界！

什么是幂律分布？

幂律分布是复杂系统的基本概念，今天我们想重点介绍什么是幂律分布，以及幂律分布的性质。

在统计学中,幂律是两个量之间的一种函数关系，其中一个量的变化将会导致另一个量的相应幂次比例的变化，且与初值无关。例如，正方形面积与边长的关系，如果长度加倍，那么面积扩大四倍。

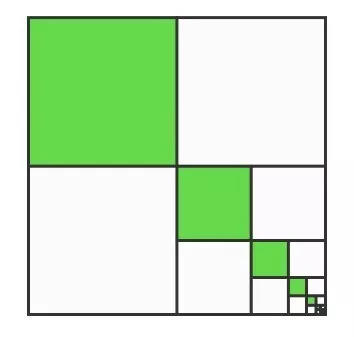
面积的幂次关系

幂律分布有什么性质？

标度不变性

（Scale invariance）

幂律分布的一个属性是它们的标度不变性。给定一个函数关系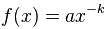，将参数 x作常量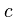的标度变换，将会导致幂函数作本身幂指数比例的标度缩放，公式表达为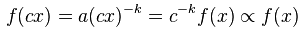：，此处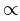，表示成正比（正比例）。

也就是说将自变量缩放常量c，那么对应函数缩放常量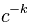。因此, 具有特定标度指数的幂律其实就等效于这个标度指数, 因为每个幂指数对应的幂律函数都只是其他情况的缩放而已。

© Marlon Figgins

如果我们取用两者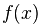（和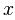）的对数，将会得到一个线性关系，呈现在双对数图上就是一条直线，这通常被看作幂律的标志。

对于实际数据, 这种线性是幂律关系数据的必要条件, 但并不是充分条件。实际上, 有许多方法可以生成模拟此指数行为的有限数量的数据, 但在它们的渐近极限中, 不是真正的幂律 (例如, 某些数据的生成过程可能遵循对数正态分布，而不是幂律分布)。

因此, 准确地拟合和验证幂律模型是统计研究中非常活跃的一个领域。

缺失完备定义的均值

（Lack of well-defined average value）

仅当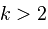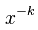，在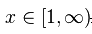具有完备定义的均值，且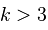时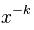，具有有限的方差。

自然界中, 大多数幂律分布的指数使得其具有完备定义的均值（K>2嘛），但其方差却无穷大，这意味着它们有可能成为“黑天鹅”行为。

假设你和你的朋友一起在一个房间里估算平均月收入，然后世界上最富有的人进入房间，他每月收入约10亿美元，那么房间里的平均收入会怎么样？

图3 富人的富裕程度会超出我们的想象

图片来源：https://www.huliwenku.com/p/ac9aqgdo.html

我们又将收入分布服从幂律现象称为帕累托分布（例如，美国人的资产净值服从指数为2的幂律分布）。一方面，这使得应用基于方差和标准差的传统统计（例如回归分析）失效。另一方面，或许能够以此为依据，采取有效的干预手段来解决一些问题。例如，可以将其应用到管理汽车尾气排放问题上，汽车尾气排放量服从幂律分布（极少数汽车导致大多数污染），那么理论上从道路上消除那些极少数汽车就足以减少总排放量。

然而，幂律分布的中位数确实存在: 对幂律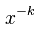，与指数k > 1，它取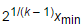，其中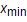是幂律所适用的最小值。

普适性（Universality）

幂律与特定标度指数的等价性在产生幂律关系的动力学过程中有更深层次的渊源。

例如, 在物理学中, 热力系统中的相变与某些量服从幂律分布有关, 它们的指数被称为系统的临界指数( critical exponents)。具有相同的临界指数的不同系统——即它们在接近临界状态(criticality)时表现出相同的标度行为——可以通过重整化理论来证明，他们的基本动力学相同。例如, 水和 CO2 在沸点上的行为在相同的普适类中, 因为它们具有相同的临界指数。

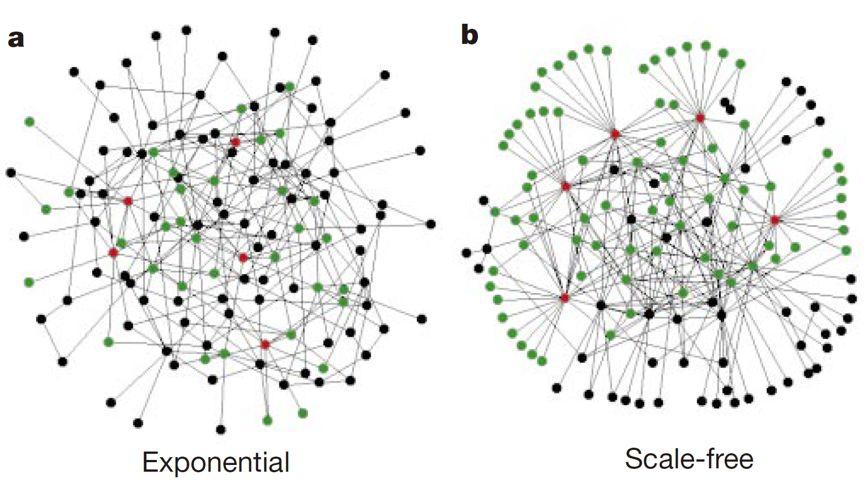
一些实际网络中的度分布可以近似由幂律分布表示

图片来源：Albert, R., Jeong, H.,& Barabási, A. L. (2000). Error and attack tolerance of complex networks.nature,406(6794), 378.

事实上, 几乎所有的物质相变都是由一小套普适类描述的。对于各种自组织的临界系统 (self-organized critical), 人们也进行了类似的观察, 虽然不是很全面, 但在这些系统中，系统的临界点是吸引子。在形式上, 这种动力学的共享性被称为普适性(universality), 而我们通常认为具有精确相同的临界指数的系统属于同一种普适类(universality class)。