“集智百科精选”是一个长期专栏，持续为大家推送复杂性科学相关的基本概念和资源信息。作为集智俱乐部的开源科学项目，集智百科希望打造复杂性科学领域最全面的百科全书，欢迎对复杂性科学感兴趣、热爱知识整理和分享的朋友加入！

今天分享网络科学领域里面社团结构这一主题。网络如何连接节点，一个个节点又怎样形成社团，本文将介绍社团结构的基本概念，有哪些好玩的案例，知名的研究者、一些入门的学习资源。

一、什么是社团结构？

二、社团结构应用

三、社团结构发现算法

四、知名学者推介

五、相关资源推介

六、集智百科词条志愿者招募

一、什么是社团结构？

“物以类聚，人以群分”。在自然界和社会中，具有相似特点的事物往往有更加紧密的联系。比如，具有相同爱好的人更易成为好友等。如果将事物以及他们之间的相互联系表示为网络，那么网络中存在的紧密连接的区域（节点集）称为社团（Community）。若网络存在社团，则称其具有社团结构（Community structure）。

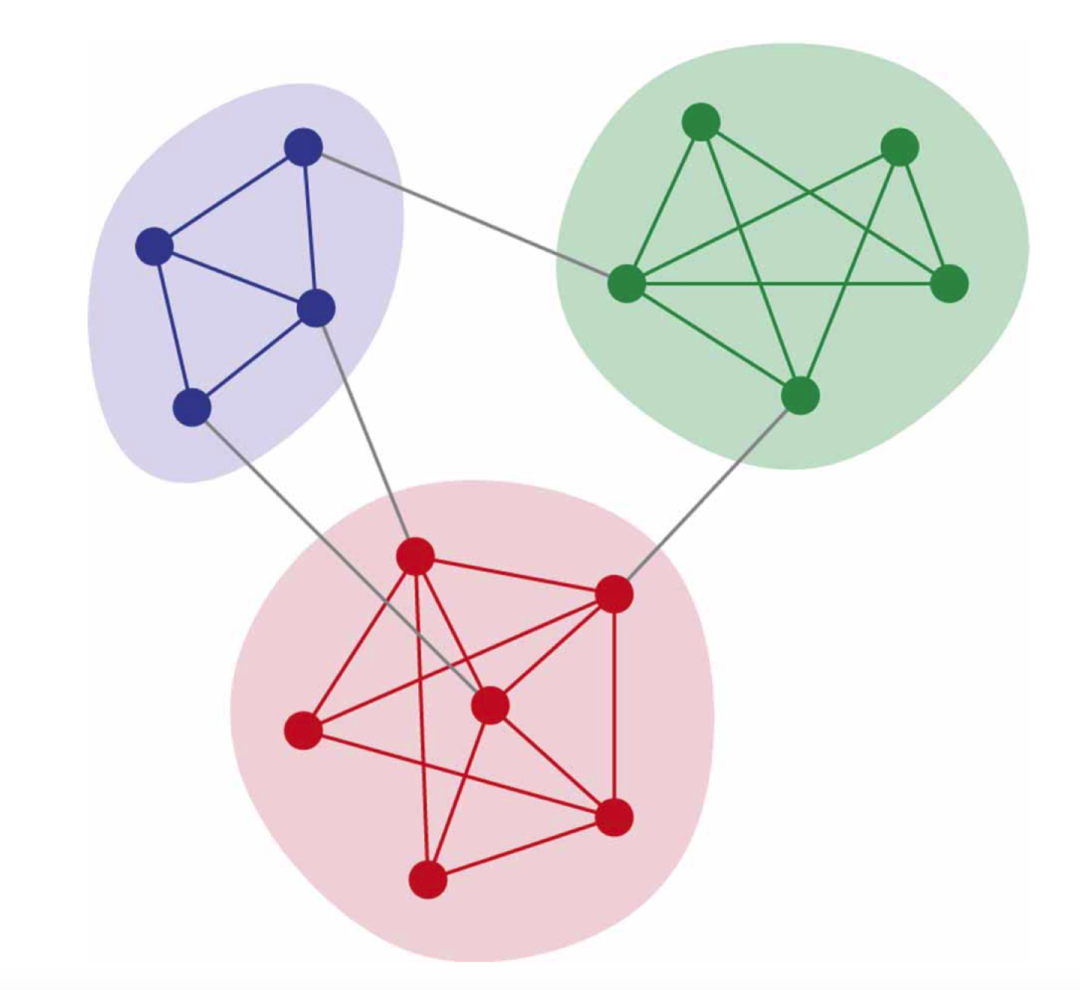
图1：社团结构示意图

社团结构普遍存在于信息网络、社会网络、生物网络等各类网络中。这些网络中的社团内部连接紧密，常对应某种特点或功能，而社团外部的连接则相对稀疏，即“内紧外松”。根据这个特点，人们可以设计算法来探测网络中的社团结构，从而更好地理解网络中蕴含的信息。

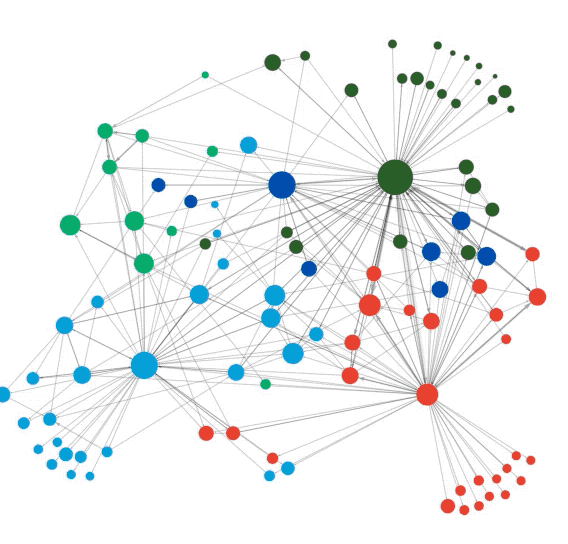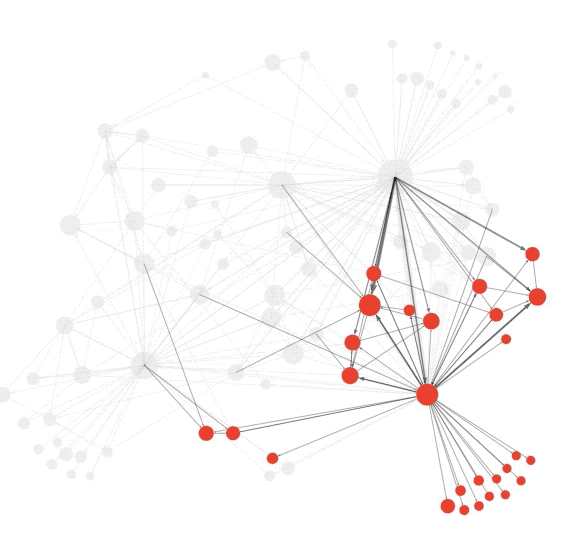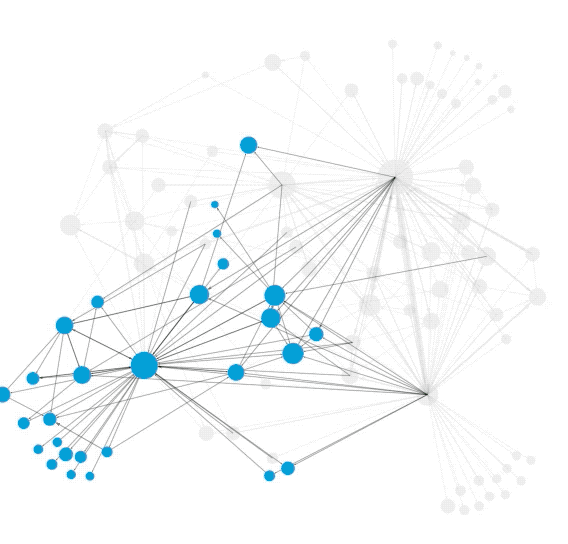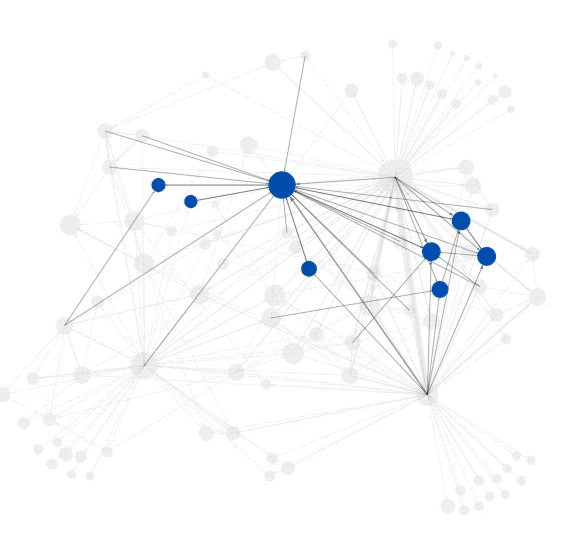
图2：社团结构可视化

二、社团结构应用

社团结构对研究复杂系统有重要价值：在人际关系网络中，社团可表示具有相似特点（如职业、年龄）的群体；在生物网络中，社团与功能模块密切相关；在论文引用网络中，社团代表了某一的研究领域等等。下面介绍几个社团结构应用实例。

领英（Linkedin）职业网络

为了研究劳动力在公司间流动的特点，学者使用领英用户的就业数据构建了一个职业网络，见下图。在网络中，节点为公司，如果职员从一个公司跳槽到另一公司，则在两公司间形成边。图中每个社团对应一种颜色。通过分析社团结构发现，劳动力的流动受地缘位置和行业特点两因素共同影响。

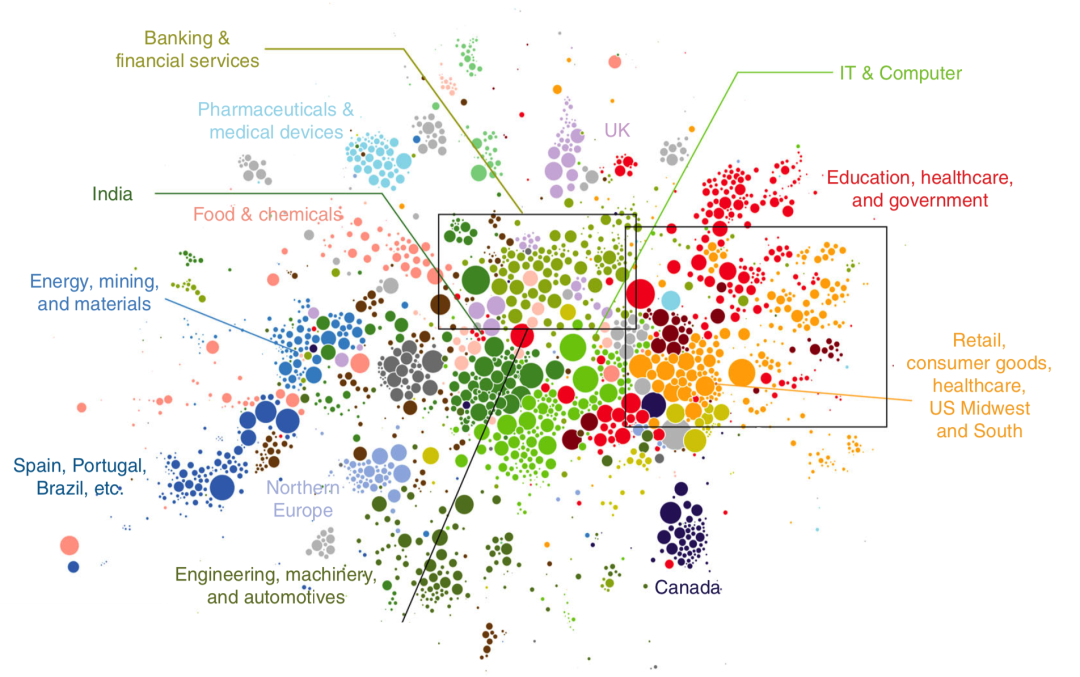
图3：领英职业网络中的社团结构

论文题目：

Global labor flow network reveals the hierarchical organization and dynamics of geo-industrial clusters

论文地址：

https://www.nature.com/articles/s41467-019-11380-w?fbclid=IwAR35Srs8_E5XN2bE0HgY8deFXC2ZCUW0BAkAowbn6A9gGCXtQryiYLbIujc

蛋白质相互作用网络

生物网络中的社团常对应“功能模块”，即参与同一生物过程或具有相似功能的蛋白质集合。例如下图蛋白质相互作用网络中包含多种功能模块（颜色对应模块）。研究发现，通过社团可以识别与与癌症相关的蛋白质，这为预测潜在致病蛋白提供了依据。

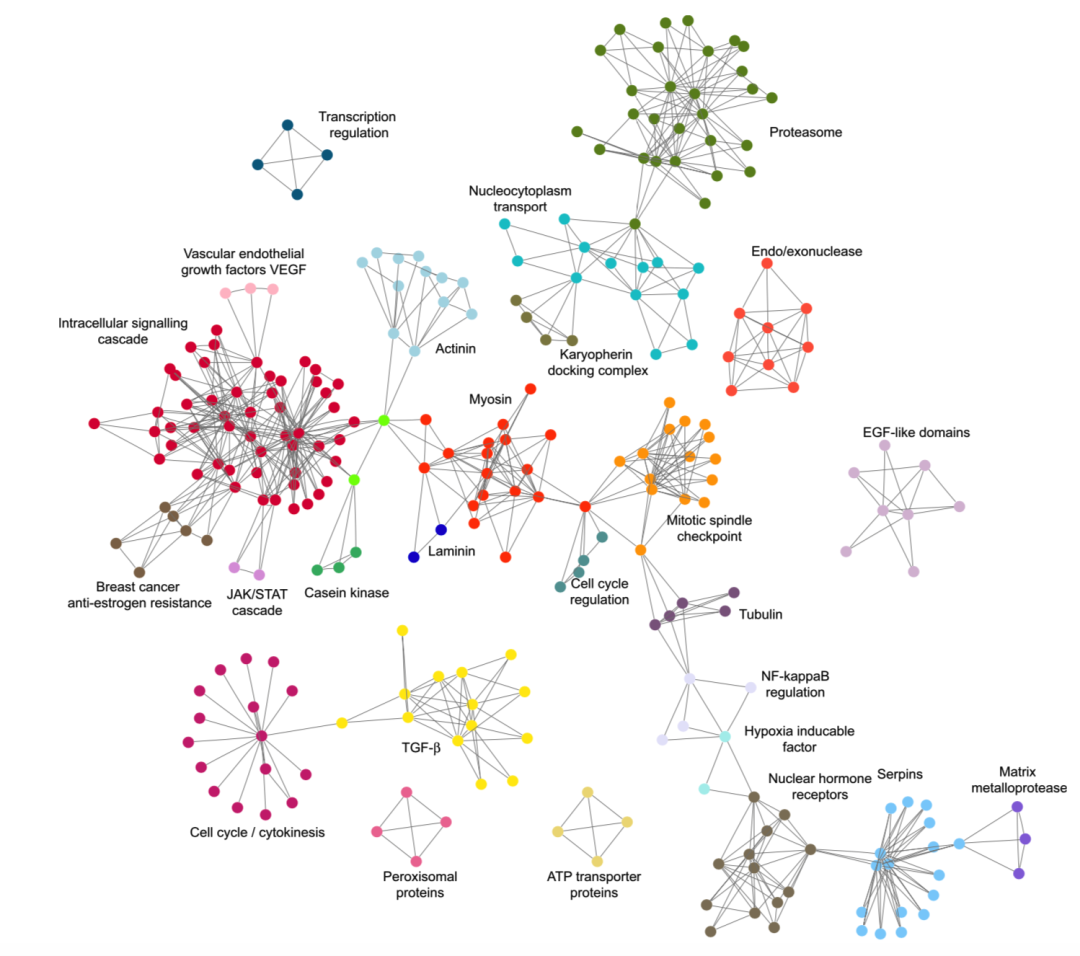
图4：蛋白质相互作用网络中的社团结构

论文题目：Community detection in graphs

论文地址：https://arxiv.org/abs/0906.0612

论文引用网络

在科学研究中，思想交流非常重要。为了描述科学家之间交流的痕迹，可以观察期刊论文之间的相互引用，构建论文引用网络。为突出论文所属的科学领域，可围绕论文引用网络中的社团构建如下科学图谱。图谱中，节点代表社团所属的领域，边为领域间的引用，箭头代表引用方向（即谁引用谁）。根据图谱，应用领域论文大多引用基础科学领域论文。

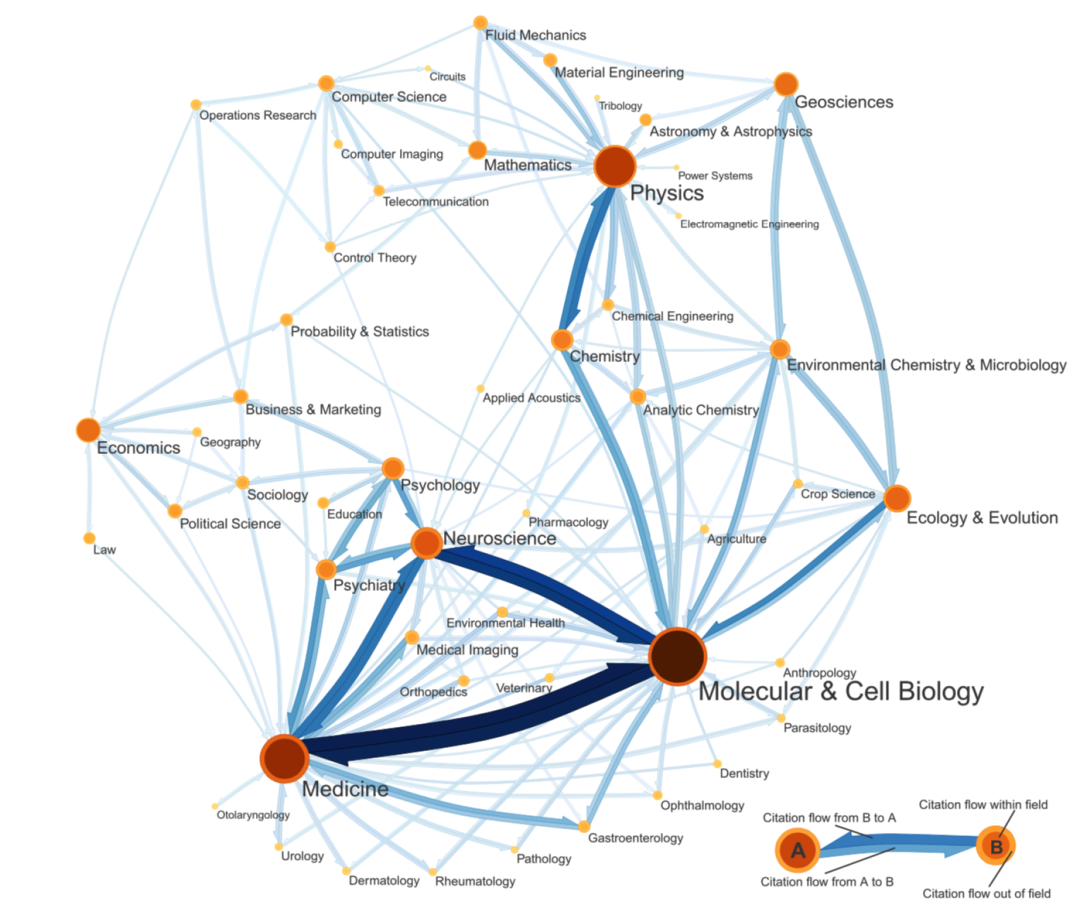
图5：基于论文引用的图谱

论文题目：Community detection in graphs

论文地址：https://arxiv.org/abs/0906.0612

三、社团结构发现算法

检测社团结构是个相对困难的任务，因为网络中的社团数目通常是未知的，且社团的大小、密度不尽相同。尽管如此，还是不断有学者发明了大量检测社团的方法，使这个领域取得了长足发展。下面列举一些经典社团检测算法。

层次聚类（Hierarchical clustering）

层次聚类是一种传统且有效的方法。它通过一种相似性度量（如欧氏距离），来计算节点间拓扑结构的相似性。然后每次找到距离最短的两个社团，然后进行合并成一个大的社团，直到全部合并为一个社团，形成一个树结构。根据需要可自行决定社团数目，得到最终结果。

Girvan-Newman 社团检测算法

另一个常见的社团检测算法是 Girvan-Newman 算法：识别各社团之间连接的边，然后去除这些边，留下的就是社团。该方法利用图论中的介数中心性（Betweenness centrality）来识别要去除的边。Girvan-Newman算法返回的结果具有较好的质量，得到广泛应用。但其运行较缓慢，不适用于上千节点的网络。

模块度最大值法（Modularity maximization）

模板度最大值法是用于使用最为广泛的社团检测算法之一。模块度（Modularity） 是一种衡量社团划分质量的标准。模块度最大值法通过搜索所有可能的分组，找到使模块度最大的分组方式作为结果。由于穷举所有可能的分组十分困难，所以实际的算法都采用近似优化方法，如贪婪算法等。

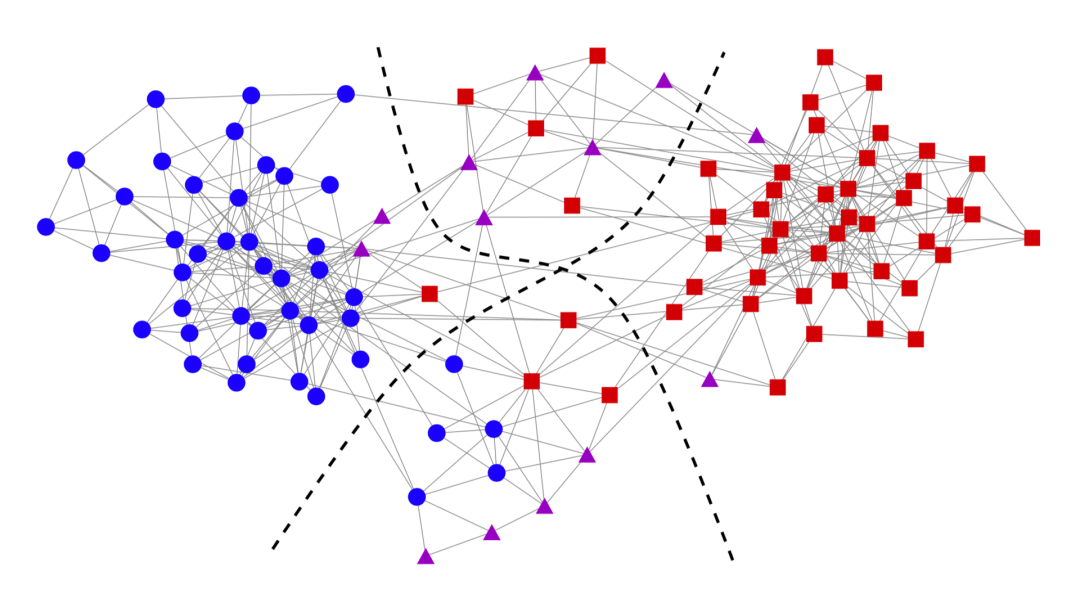
图6：模板度最大值法检测社团结构

注：使用网络科学工具包NetworkX , 可以轻松调用上述三种算法，实现社团检测。

四、知名学者简介

Mark Newman

图7：Mark Newman

美国密歇根大学物理系和复杂系统研究中心特聘教授。同时也是圣塔菲研究所（Santa Fe Institue）外聘教授。网络科学的先驱者之一，2014年被授予拉格朗日奖。他的论文总引用量超过18万，著有网络科学经典著作《Networks: An Introduction》。

在社团检测领域，他提出了模块度最大值算法，是使用最广泛的算法之一。

Santo Fortunato

图8：Santo Forunato

美国印第安纳大学Bloomington分校信息学、计算和工程学院教授。印第安纳大学网络科学研究中心主任。论文总引用量超3万，其中最著名的论文为2010年发表的”Comunity detection in graphs”，引用量超8000，是社团检测领域的经典综述之一。

五、相关资源推荐

经典文献

S. Fortunato (2010). “Community detection in graphs”. Phys. Rep. 486 (3–5): 75–174. arXiv:0906.0612.

M. Girvan; M. E. J. Newman (2002). “Community structure in social and biological networks”. Proc. Natl. Acad. Sci. USA. 99(12): 7821–7826. arXiv:cond-mat/0112110.

M E J. Newman (2006). Modularity and community structure in networks[J]. Proceedings of the national academy of sciences, 103(23): 8577-8582.https://www.pnas.org/content/pnas/103/23/8577.full.pdf

课程

复杂网络中的社团结构

该课程中主要讲解了网络中集团结构的定义，以及层次聚类法、GN 聚类法的思想，从中观尺度——社团结构去探索复杂网络的性质。