导语

网络是认识世界的强力手段，图论则是网络科学的数学基础，但两个领域近年来的结合并不密切。来自中欧大学的网络科学研究者，在Nature子刊Communications Physics上发表文章 Bridging the gap between graphs and networks，讨论如何将网络科学解决现实问题的经验引入图论运营，同时将图论中的前沿数学成果带入网络科学。在数据驱动下，架起图与网络之间的桥梁，网络科学将有机会迎来更大的突破。

本文首发自集智斑图，完整论文资料清单请扫码获取：

网络科学已经成为描述真实世界中复杂的物理、生物、社会和技术系统的结构和动力学的一个有力工具。网络直观和灵活的特性促进了网络科学的普及，其主要基础是解决相互作用的异质性、时间性和适应性模式时的经验观察。图论由于在随机图演化方面的开创性工作，经常被认为是网络科学的数学基础。尽管如此，研究这两个领域的团体在很大程度上却仍然缺乏联系。

在这篇评论中，我们讨论了领域之间进一步交流，在图与网络之间搭建桥梁的必要性，以及网络科学将如何从这种影响中获益。更加数学化的网络科学或许可以阐明随机性在建模中的作用，为潜在的行为规律提供线索，并预测自然界中尚未观察到的复杂网络现象。

1. 为网络化现实构建数学理论

在人类科学发展史的背后，有一个故事是关于数学理论建构。在建构数学理论的过程中，科学家不仅通过实验和数据分析来揭示经验现象的行为，也会发展理论以数学的语言将这些行为抽象化。当数学与现实“充分同构”时，这个过程就等同于科学理解；当理论虽然忽略了一些特征，但仍然包含了被认为是最重要的机制时，这个过程也仍然允许我们通过逻辑推断来准确地描述感兴趣的现象。数学与现实在结构上的充分相似性使得科学家能够预测事件，控制自然系统，甚至预测那些尚未被经验证实的行为。

直到不久之前，对于现实的数学表示的科学努力大多集中在“最简单”的自然系统的元素上，或者是在最小尺度上——组成微观世界的物理、化学和生物实体，或者是在最大尺度上——热力学系统和宇宙的大尺度结构。这些努力之所以取得成功，一方面得益于可获得可重现数据，另一方面则是由于可以部分忽略系统的组成部分及其相互作用的变化，同时仍然保持理论的精确性。

主要是在过去几十年里，科学家们才探索了元素处于“介观”尺度的现象的数学——大脑和生物体的生理，生态系统，以及现代世界的社会、技术和经济结构。这些系统本质上很复杂，因为其组成部分之间（变化且通常是自适应的）相互作用是充分同构的数学理论的基本特征。因此，任何框架如果忽略元素的异质性或相互作用，都将无法准确地描述和预测复杂的相互作用系统的行为。

正是由于对组成部分及其相互作用进行数学描述的需要，才促进了网络科学的兴起，使其成为定量化地描述复杂系统的结构和动力学的一种跨学科努力。网络，也就是一组元素或者说“节点”的集合，这些节点由它们的相互作用，也就是“边”连接起来。在大数据革命的推动下，网络这一概念已经成为描述对物理、生物和社会现象的无数经验观察的强大工具。

与网络类似，图是由若干顶点和连接这些顶点的边构成的图形，研究图的数学分支也就是图论。受社会学和经济学中开创性研究的启发，网络科学从图论中继承了其最初的概念。然而自此之后，图论和网络科学就分道扬镳了，无论是它们研究的问题，还是研究它们的学术团体都几乎没有重叠。

图论专注于为图的性质提供严格的证明，例如图的枚举、着色和覆盖，应用范围涉及到从化学到电路设计等诸多不同领域。与之相反，当前的网络科学更类似于物理学中的唯象理论，它专注于对真实世界网络的观察，并以必要的数学概念来量化它们，目的是对其底层生成机制有一个直觉的理解。图论由于其目标是追求严谨的论证，目前更多致力于研究可分析求解的结构，如随机图或稠密图；而网络科学关注数据中最普遍的特征，如大型且有限网络中结构与时序行为的稀疏性和异质性。

图1：英国数学家J. J. Sylvester在1878年的一篇Nature论文中，首次将“graph”作为术语提出。

我们认为，图和网络之间的差异并非不可逾越的鸿沟，而是连接这两个学科的前所未有的契机：将网络科学中由经验驱动的问题引入图论，同时也将图论中的陌生成果带到网络科学中。通过广泛的跨学科项目，如欧洲研究委员会的协同资助项目”DYNASNET“（Dynamics and Structure of Networks），科学家们希望将图论中有趣的概念（如表示集合与极限对象）与网络科学中的“大创意”联系起来，后者包括异质性，结构和动态相关性，社团与介观尺度的序，以及网络动力学与网络上的动力学之间的耦合。

随着时间的推移，物理学的一些领域变得越来越数学化，这些努力将为量化网络科学中的经验结果所需的数学构造带来形式和精确性。与此同时，图论学家将面临网络科学家在分析网络控制、物理网络或具有高阶相互作用的网络时带来的新的理论挑战。我们相信，这种协同作用将提高这两个学科对自然和社会的复杂网络系统进行定量预测的能力。

2. 从数学物理中学习

从最初的天体理论和牛顿力学，到电磁学、相对论和量子场论，物理学历史上一个著名的挑战是，建立一个数学框架来揭示经验科学中的逻辑一致性。首先，有一些普遍的观测结果，它们被可重复的数据和实验所支持，接着通常由于先前接受的理论中存在不一致性，从而激发了数学描述的尝试。在更精确的观测结果和更复杂的数学描述之间通常会形成一个反馈回路，最终形成具有预测能力的数学理论。

在电磁学中，法拉第和其他人高超的实验技巧最终通向了具有严格数学框架的麦克斯韦方程，而麦克斯韦方程反过来预言了光速的不变性，并为爱因斯坦相对论提供了最初的灵感。在统计力学中，肯尼斯·威尔逊（Kenneth Wilson）发展了重整化群的方法来推导在临近连续相变时观察到的（一个普适类中）临界指数的彼此吻合，解释了为什么热力学系统的某些特征不会因为微观细节的不同而变化。如今，偏微分方程和随机微分方程的数学理论在物理学中广泛出现，在电磁学、统计力学、流体力学、声学、弹性理论、天体物理学等领域都有应用。

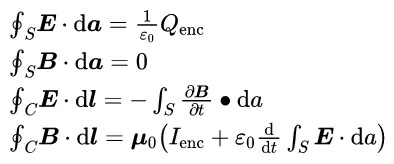
图2：最美的公式——麦克斯韦方程组

一个精确的数学理论甚至可以指明要在哪里寻找新物理。例如，诺特定理描述了系统的对称性和守恒量的相关性——如果系统中存在一种对称性，那必然存在着一个守恒量与之对应，反之亦然。例如，动量守恒与空间的平移不变性相对应，能量守恒则与时间的均匀性相对应。诺特定理源于对拉格朗日和哈密顿力学中运动常量的分析，并发展成一个强大的工具，可以找到让物理学定律在时间和空间中保持不变的变换。

诺特定理：

https://zh.m.wikipedia.org/zh-cn/%E8%AF%BA%E7%89%B9%E5%AE%9A%E7%90%86

网络科学和图论领域中与实证发现最相关的发展已经做出了尝试，并发展出了严格的数学框架，它们最初被现实世界的观察所激发，结果帮助我们对复杂网络系统底层机制之间的相似性形成了有价值的理解。对随机图的分析表明，平均路径长度（网络中将任何两个节点联系起来的最短路径的平均值）随网络规模缓慢地增长，也就是通常所说的“小世界”效应，不仅在大多数真实网络中普遍存在，甚至在边（的生成概率）遵循伯努利分布这种最简单的情况下也会出现。反过来，对大尺度的社会、生物和技术网络的探索促使科学家为这种数学上的形式主义创造替代方案，以解释实际观察到的特征，如度的异质性、高聚集性和社团结构。

广义相对论将引力场解释为时空的弯曲，认为物质的分布决定了时空的几何结构。受此启发，网络科学家也探索了将网络嵌入双曲空间与从中出现结构相关性和异质性之间的关系。发现几何与网络结构之间的联系可能会立即产生实际应用，例如，对底层空间中距离的新认识可以增强网络的导航能力。

3. 数学化的网络科学

在未来会有哪些突破？

受到对于大尺度现实世界网络的众多发现的激励，在下面我们将描绘一系列未来的突破，这些突破可能有助于在图论的形式表述和网络科学的数据驱动的直觉之间搭建桥梁。我们推测，这些突破将导致网络科学像标准的物理理论一样，朝着更加数学化的方向发展，这将为全面地理解复杂网络系统提供数学基础。

（1）稀疏图的极限对象

有越来越多的文献在研究稠密图序列及其伴随的极限对象“图极限”（Graphon，可以理解为是一个内在结构恒定的随机图，在顶点数趋于无穷时所收敛到的极限）的性质。图极限有助于简化一些定理的公式和证明，如与图的距离、子图采样、图序列收敛等相关的定理。然而，大多数真实世界的网络不是稠密而是稀疏的，节点之间的边相对较少。一旦图论能够描述稀疏图序列的经验相关的渐近性行为，这些结果将在网络科学和复杂系统预测中得到应用。有前景的极限对象包括“Graphing”（度有界的图的极限）和“Graphex”（作为随机度量的图的极限）。

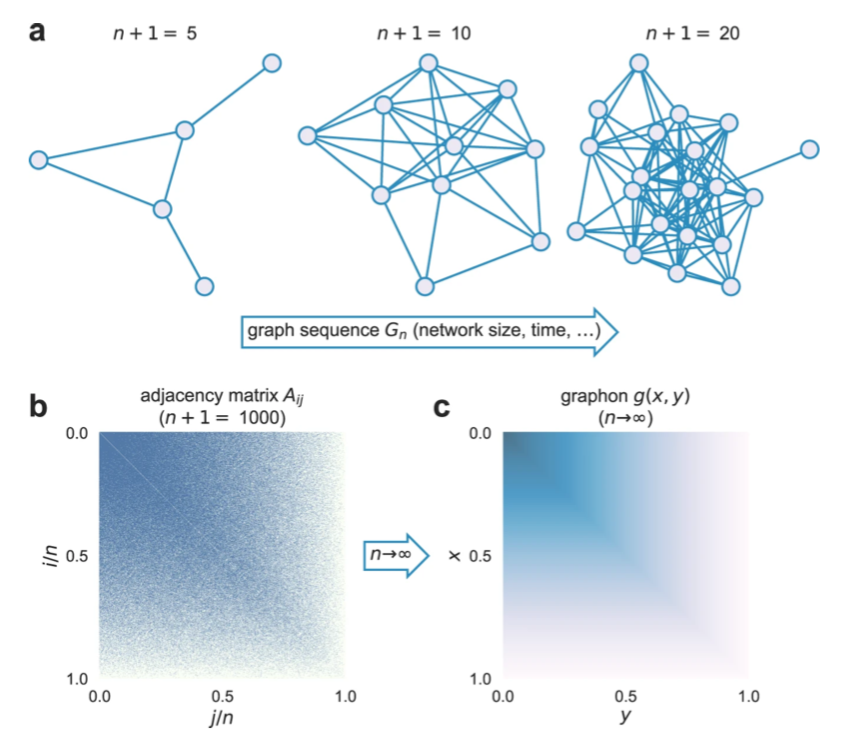
图3：（a）一个正在生长的大小为 n+1 的图 Gn。从 n = 0 时的单个节点开始，在每一次迭代中，增加1个节点，并以 1/n 的概率连接所有非相连的节点对。这是稠密网络的一种简化的优先连接机制，让人想起那些有争议地推动实际的无标度网络增长的机制。

（b）n 较大的邻接矩阵 Aij（节点标签 i, j = 0，…，n−1）表明，旧节点（i≪ n）如何比新节点连接更紧密。

（c）在 n→∞ 的极限情况，Aij 趋于“graphon” g(x, y) = 1−max(x, y)，其中 x 和 y 由 i = xn 和 j = yn 给出。通过考虑极限对象而不是有限大小的网络，许多与网络结构有关的问题都可以更容易地表述和解决。

（2）结构和时间异质性的稀疏图理论

研究稀疏极限对象时还可以考虑网络科学中广泛记录的其他结构和动态约束。真实世界的网络在几个尺度上显示出异质结构，在核心外围和社团中存在介观模式。实际的网络也是时间性的，因为节点和边可以随着不均匀且不必然确定的动态而出现和消失。我们期待图论的进步，如随机块模型网络的极限对象，对序列指标是时间而不是图的大小的图序列的分析，以及稀疏图的随机矩阵理论。

（3）对网络和网络的动态过程的理解

网络科学的很大一部分研究的是网络结构对动态过程的影响，如疫情传播、信息传递和同步等。一个相关的话题是网络本身的动态：网络的生长和衰退、边的重新连接、时序网络以及适应性网络。目前的方法包括网络动力系统理论、线性稳定性分析和矩阵谱理论。

然而，我们仍然需要实际经验相关的网络动力学的数学思想，特别是当网络上的动力学和网络的动力学具有相似的时间尺度，或者当网络是多层的或具有高阶相互作用时。我们相信，代数几何、计算拓扑和图极限理论的进展将有助于克服这一困难。

4. 搭建图与网络之间的桥梁

科学家如何才能实现这些理论突破，从而搭建起图论与网络科学之间的桥梁？我们不妨再一次从数学物理的历史中搜寻线索。

在热力学的早期阶段，卡诺、克劳修斯和开尔文这些人发现了大型物理系统的可测量量之间的唯象关系，但对深层的动力学还没有完全理解。然后，玻尔兹曼、麦克斯韦和吉布斯这些巨人用概率论从微观力学定律中推导出这些关系，表明宏观现象是更小尺度上那些更基本过程的统计结果。

我们注意到，当前的网络科学与19世纪的热力学处于类似的状态，有许多观测结果和简化的唯象模型。如果在图论与网络科学之间建立更强的连接，研究人员就能够改进对网络现象的理想化假设，与现实世界的应用保持更高的相关性，发现这些微观机制和大尺度行为间的数学联系。

在接下来的几年里，“DYNASNET”的成员（以及即将开展的类似项目）将尝试各种方法来搭建图论和网络科学研究之间的桥梁。一种可能是使用图论的结果作为网络科学中微观行为规律的选择原则，正如诺特定理指出，存在许多类假想的拉格朗日算子来描述一个经验不变量。这些原则不仅会使建模工作更高效，而且会突显出表面看似无关、实则由相同的深层机制驱动的现象。与之相对，图论中的极限对象可能会导致网络版本的中心极限定理：尽管许多大尺度复杂系统的组成元素和相互作用各不相同，但这些系统特征的数学推导过程是相似的。

另一种可能是进一步探索随机性在复杂网络系统中的作用。网络科学家用随机性来代替那些未知的相互作用规则，然后大多通过数值和数据驱动的模拟来推断宏观行为。经过实际经验调整的图理论结果——例如塞迈雷迪正则性引理（Szemerédi’s regularity lemma）——或许会揭示出现实世界网络中随机性、结构和动力学之间的基本相互作用。

注释：塞迈雷迪正则性引理是研究稠密图的有力工具。粗略说来，该引理断言，对于任意一个足够大的图，都可以将其顶点集划分成若干个差不多同样大的子集，使得几乎每两个不同子集之间的边，都具有随机二分图的性质。

未来，研究人员和具有科学头脑的政策制定者或许可以利用这些进展，对尚未观测到的复杂网络现象进行定量预测。

网络控制理论已经在秀丽隐杆线虫的连接体中发现了以前未知的与运动行为有关的神经元。当前的事件表明，网络流行病学正在逐步达到一定的能力，可以对全球流行病爆发（包括COVID-19大流行）进行业务预测，并预测旅行限制等紧急政策的影响。源自图论和网络科学的一些未来预测甚至可能追随巨大的理论成就的脚步，比如标准模型中希格斯玻色子的发现，或者广义相对论中引力波的存在。

如果网络真的是物理现实在介观尺度上的一个基本特征，如我们许多人所相信的那样，那么关于网络存在的未被发现的结果应当无处不在。我们预计，这些未来的发现将把看似遥远的学科连接起来，形成一个由数学锤炼而成的包罗万有的科学知识网络。