随机反应网络描述了化学物质通过一系列反应的变化,被广泛用于模拟物理、化学和生物等复杂系统中的随机过程。随机反应网络通常通过化学主方程进行建模,它描述了物种分子数的联合概率分布随时间的演化。然而,系统可能状态数随着物种的种类数呈指数增长,因此,获得物种分子数随时间演化的联合概率分布是一个难题。
2023年3月16日,北京师范大学复杂系统国际科学中心的汤迎副研究员和学生翁佳钰、与中国科学院理论物理研究所的张潘研究员合作,在 Nature Machine Inttelligence 杂志发表论文“Neural-network solutions to stochastic reaction networks”,提出了使用变分自回归网络来求解化学主方程的机器学习方法。该方法能跟踪联合概率分布的时间演化,在多个物理学和生物学中的代表性例子中得到应用。
关键词:随机反应网络,化学主方程,变分自回归网络,随机过程
翁佳钰 | 作者
汤迎、张潘 | 审校
邓一雪 | 编辑

论文题目:
Neural-network solutions to stochastic reaction networks
论文链接:
https://www.nature.com/articles/s42256-023-00632-6
随机反应网络是物理学、化学、生物学和生态学中随机过程的标准模型。代表性的例子包括生灭过程、自发不对称合成模型和基因调控网络。特别地,由于在单细胞水平上测量分子的技术正快速发展,对分子数量少且易受随机噪声影响的细胞内反应网络的研究变得愈发重要。处于充分混合条件下的随机反应网络可以通过化学主方程 (CME) [1]建模,它描述了物质分子数随时间演化的联合概率分布。然而,物种分子数状态空间的大小随着物种的种类数增多呈指数型的增大;因此,准确表示联合概率并求解CME具有挑战性。
为了通过数值方法近似求解CME,研究者已经做出了许多努力。最常用的方法,Gillespie算法[2]作为一种动力学蒙特卡罗方法,从所有可能的状态轨迹中采样以生成相关变量的统计数据。然而,为了获得高精度的联合概率分布数据需要进行大量的轨迹模拟,并且系统的动力学可能会受到罕见但重要的轨迹的显著影响,而这些轨迹很难通过Gillespie算法进行采样。
与基于采样的方法不同,研究者也提出渐近近似方法将CME转换为连续状态方程,例如化学Langevin方程[3]。这种方法的计算效率更高,但是当物种的分子数有很大波动时,连续状态近似的方法就变得不准确。
另一类方法通过对CME的状态空间进行截断,覆盖大部分概率分布来获得数据,包括Finite state projection[4],ACME[5]等方法。然而,当物种的种类数和分子数都变大时,这些方法的计算成本仍然很高,难以达到高精度[6]。
尽管在这一方面已经付出了很大的努力,但我们仍然缺乏一种通过直接表示联合概率分布演化的方式来求解化学主方程的通用方法。
在文章中,作者开发了一种神经网络方法来研究随机反应网络中物种分子数的联合概率分布。该方法受到神经网络对高维数据的强大表示能力的启发,利用变分自回归网络(VAN)[7] 来求解CME(图 1)。VAN已被应用于统计物理学、量子多体系统、开放量子系统、量子电路和计算生物学,它能够对物种分子数构型进行有效采样,并计算不同构型的归一化概率。
文章扩展了VAN以表征随机反应网络中物种分子数的联合概率分布。作为VAN的神经网络单元,作者采用了递归神经网络 (RNN) [8]和Transformer架构[9],它们可以灵活地表示高维概率分布并灵活调整物种分子数的上限。拓展的VAN也允许对每个物种添加物种分子数上限的约束,或者维持某些系统中物种分子总数守恒的约束,这都可以收缩概率空间以提高计算的准确性。
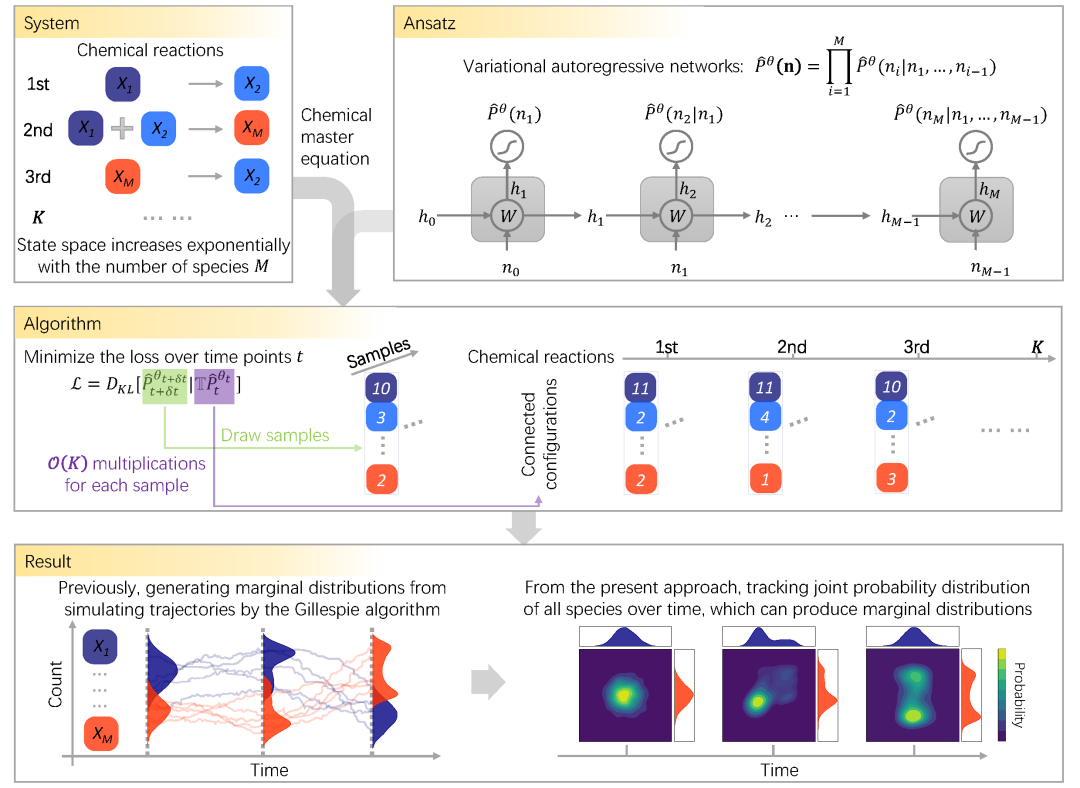
图1:跟踪随机反应网络随时间变化的联合概率分布。(上)对于反应网络,状态空间随物种的种类数增多呈指数级增大,使得跟踪联合分布的时间演化变得困难。变分自回归方法(VAN)可以参数化表示联合分布。(中)从初始分布出发,通过连续时间步长的联合分布之间的KL散度来最小化损失函数,以学习其时间演化。为了在下一时刻训练VAN,从上一时刻分布中抽取样本。每个样本都由一列堆叠的正方形表示,其颜色代表物种,数字表示它们的分子数。对于每个样本,连接构型的数量与化学反应的数量相等。(下)用Gillespie算法模拟轨迹可以产生边际分布,但一般不能准确产生高维联合分布,而VAN跟踪了所有物种数随时间变化的联合分布。
文章的方法与最近提出的基于神经网络的方法有很大不同,相比于使用从Gillespie算法得到的数据来训练神经网络的方法[10,11],训练自回归网络采用强化学习框架中的策略梯度算法,不需要使用其他方法先验模拟的任何数据。该方法给出了一个自动归一化分布作为任意有限时间内CME的解,所得到的联合分布,提供了高维状态空间中每种构型的概率。
作者将该方法应用于物理学和生物学中的代表性示例,并证明它可以准确地生成随时间变化的概率分布。具体的应用包括基因切换开关,细胞内信号级联反应、早期生命自我复制,以及具有时变速率的流行病模型等。
边际分布统计结果与使用先前的数值方法得到的结果相符,例如Gillespie算法或Finite state projection方法。该方法有效地产生联合概率分布的时间演化信息,特别地,变分自回归网络在表示多峰分布方面表现出可塑性,对于物种分子数守恒的系统,具有随时间变化的反应速率的系统和高维系统均是有效的。结果证明该方法是一种基于现代机器学习研究随机反应网络的通用方法。下面展示了该方法在遗传基因切换开关(图2)和细胞内信号级联反应(图3)的结果。
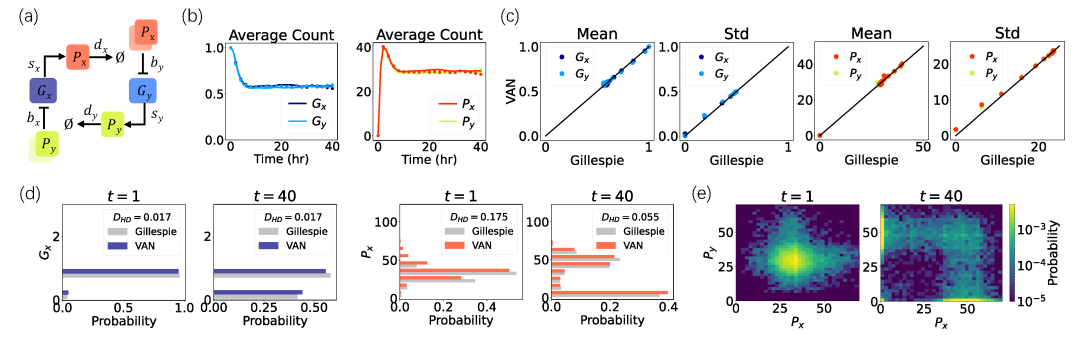
图2:基因切换开关的结果。(a) 随机反应网络的示意图。(b)由VAN(点)和Gillespie算法(线)得到的基因和蛋白质的平均分子数随时间的演化。(c)比较VAN和Gillespie模拟在时间点t = 0,1,…,40的基因和蛋白质的均值和标准差。(d)Gillespie模拟(灰色)和VAN的边缘分布。图例中包含两个分布之间的Hellinger距离。(e)由VAN得到的两种蛋白质在时间点t = 1,40的联合分布,颜色对应对数尺度上的概率值。
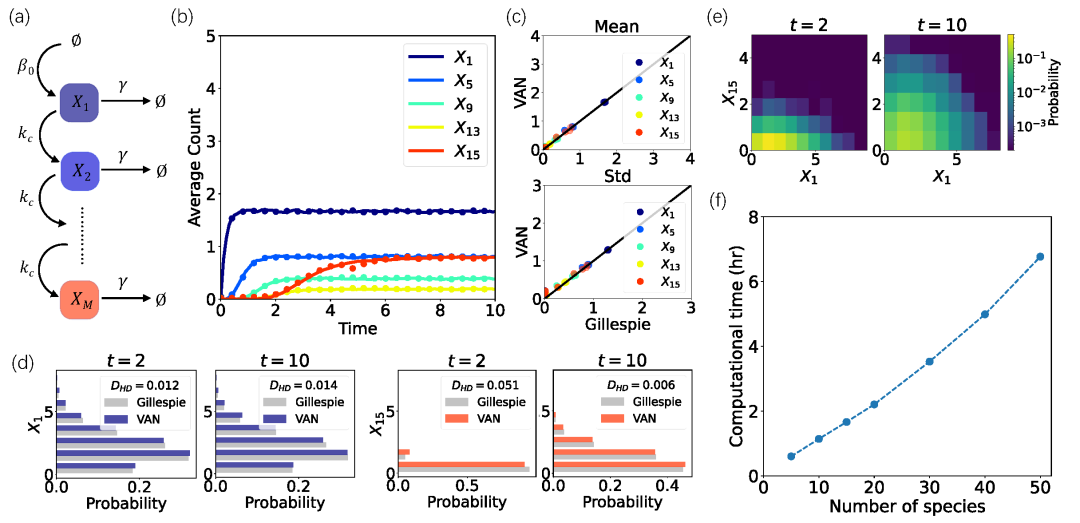
图3:细胞内信号级联反应的结果。(a)随机反应网络的示意图。(b)由VAN(点)和Gillespie算法(线)得到的基因和蛋白质的平均分子数随时间的演化。不同颜色表示不同物种种类。(c)在时间点t=1,2,…,10,VAN和Gillespie模拟之间物种分子数的平均值和标准差的比较。(d)Gillespie模拟(灰色)和VAN的边缘分布。图例中包含两个分布之间的Hellinger距离。(e)第一个物种和最后一个物种在VAN时间点t = 2,10的联合概率分布,颜色对应概率值。(f)物种种类数不同的系统的计算时间,可以发现计算时间尺度几乎与物种的种类数成线性关系,该方法对于高维系统有高效的计算效率。
文章提出了一种机器学习方法来跟踪随机反应网络,通过利用变分自回归神经网络来求解化学主方程中的联合概率分布。作者将它应用于生物物理学、系统生物学和流行病的模型中,结果表明该方法可以准确地跟踪随时间变化的联合概率分布,并且在具有多峰分布、物种分子数守恒、含有时变速率或高维系统中均是有效的。这套计算框架普遍适用于随机反应网络分析,可用于获得一般的随机反应网络中物种联合概率分布的时间演化。
论文链接:https://www.nature.com/articles/s42256-023-00632-6
论文免费只读版本:https://rdcu.be/c7MVp
程序包:https://github.com/jamestang23/NNCME
参考文献
[1] Bressloff P C 2014 Stochastic Processes in Cell Biology (Springer)
[2] Gillespie D T 1976 A general method for numerically simulating the stochastic time evolution of coupled chemical reactions Journal of Computational Physics 22 403–34
[3] Gillespie D T 2000 The chemical Langevin equation J. Chem. Phys. 113 297–306
[4] Munsky B and Khammash M 2006 The finite state projection algorithm for the solution of the chemical master equation J. Chem. Phys. 124 044104
[5] Cao Y, Terebus A and Liang J 2016 Accurate chemical master equation solution using multi-finite buffers Multiscale Model. Simul. 14 923–63
[6] Gupta A, Schwab C and Khammash M 2021 DeepCME: A deep learning framework for computing solution statistics of the chemical master equation PLOS Computational Biology 17 1–23
[7] Wu D, Wang L and Zhang P 2019 Solving Statistical Mechanics Using Variational Autoregressive Networks Phys. Rev. Lett. 122 080602
[8] Hibat-Allah M, Ganahl M, Hayward L E, Melko R G and Carrasquilla J 2020 Recurrent neural network wave functions Phys. Rev. Research 2 023358
[9] Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez A N, Kaiser Ł and Polosukhin I 2017 Attention is All you Need Advances in Neural Information Processing Systems vol 30, ed I Guyon, U V Luxburg, S Bengio, H Wallach, R Fergus, S Vishwanathan and R Garnett (Curran Associates, Inc.)
[10] Jiang Q, Fu X, Yan S, Li R, Du W, Cao Z, Qian F and Grima R 2021 Neural network aided approximation and parameter inference of non-Markovian models of gene expression Nat. Commun. 12 1–12
[11] Sukys A, Öcal K and Grima R 2022 Approximating solutions of the Chemical Master equation using neural networks iScience 25 105010
AI+Science 是近年兴起的将人工智能和科学相结合的一种趋势。一方面是 AI for Science,机器学习和其他 AI 技术可以用来解决科学研究中的问题,从预测天气和蛋白质结构,到模拟星系碰撞、设计优化核聚变反应堆,甚至像科学家一样进行科学发现,被称为科学发现的“第五范式”。另一方面是 Science for AI,科学尤其是物理学中的规律和思想启发机器学习理论,为人工智能的发展提供全新的视角和方法。
集智俱乐部联合斯坦福大学计算机科学系博士后研究员吴泰霖(Jure Leskovec 教授指导)、哈佛量子计划研究员扈鸿业、麻省理工学院物理系博士生刘子鸣(Max Tegmark 教授指导),共同发起以“AI+Science”为主题的读书会,探讨该领域的重要问题,共学共研相关文献。读书会从2023年3月26日开始,每周日早上 9:00-11:00 线上举行,持续时间预计10周。欢迎对探索这个激动人心的前沿领域有兴趣的朋友报名参与。
推荐阅读

















