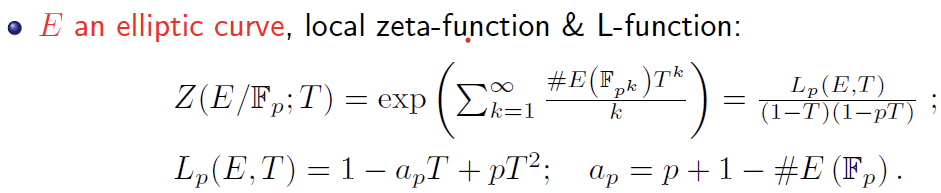20世纪,许多伟大的数学家与物理学家,比如爱因斯坦、陈省身、杨振宁,都预示到微分几何、代数几何、拓扑学或者表示论等数学分支是现代物理的必须语言。例如,引力是 tangent bundles 上的 Ricci 2-形式。我们用了一个世纪把许多物理理论翻译成了数学语言,涉及到的数学分支包括(纯和计算)几何学、群论、组合数学,以及数论。
21世纪第一个十年,随着数据的兴起,Sage, M2, GAP, LMFDB, GRDB 作为工具,进入了纯数学和数学物理的研究之中。
人工智能是21世纪的第二个十年研究数学物理和纯数学的新工具。
超弦理论(string theoy)是一种十维的量子场论。在十维时空中,它统一了广义相对论和量子场论。我们生活在四维时空,对于多出来的六维,八九十年代,一批数学家就意识到它有一个很简单的解,即一个三维复流形。这个解把量子场论与广义相对论结合的问题变成了一个新的问题,也就是怎么去理解所有的三维复流形。不管这个几何是什么,不同的几何给一个不同的四维宇宙,这个宇宙是不是都像我们的宇宙呢?我们不得而知。但无论如何,我们宇宙中所有的物理,比如基本粒子和它们之间的相互作用,都可以用这个六维流形上的数学来表达。比如,粒子就是上同调理论,质量就是流形上的尺度问题,Yukawa complex 就是流形形式之间的积分形式(integral form)问题。从某种角度上来说,超弦理论是对开普勒以前提出的一个神秘问题的很好回答。开普勒以前说只要有物质,那里就必须有几何。
我们怎么去理解我们的宇宙呢?有三种哲学的方法。第一种是我们的宇宙是完全随机的,我们观察到宇宙是这样,因为我们在这观察的宇宙是这样。第二种是我们的宇宙是很特殊的,至今我们还没找到一种选择原理。最后一种是说,我们的宇宙是多重宇宙中的一个。现在,超弦理论很大一部分是在这三种不同的哲学中徘徊。
超弦理论最大的一个挑战叫做真空简并(vacuum degeneracy)问题,即怎样在不同的几何中找到一个能产生我们这样的宇宙的几何。Douglas 在2003年研究过超弦在所有真空里的统计行为。同时,KKLT(Kachru-Kallosh-Linde-Trivedi (2003))发现如果去找这些几何的话,需要在10500的数据里去找。为什么要这么大的数据呢?基本原因是超弦理论需要代数几何来做,代数几何需要组合几何来做,而一进入组合数学的范畴,就会有超指数的维度增长。
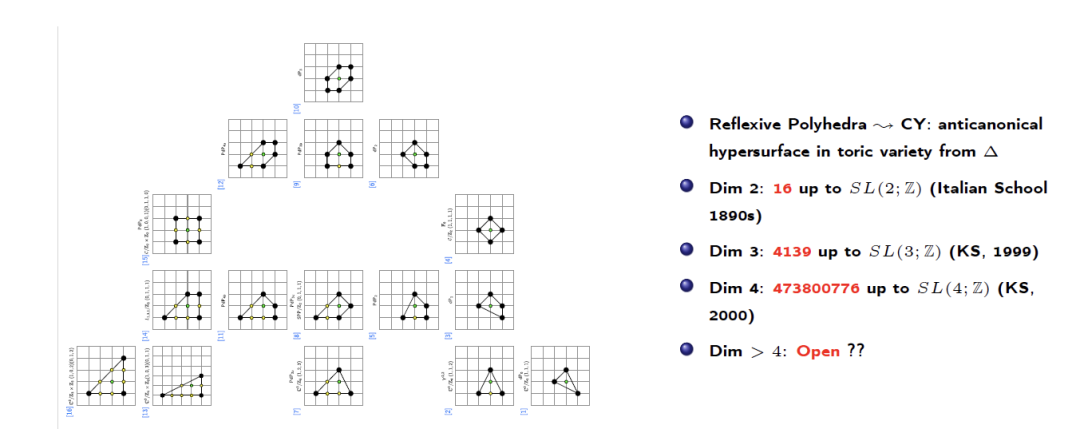
例如,基于Borisov-Batyrev的一个定理,最简单的构造卡拉比丘流形的方法就是用自反多面体(reflexive polyhedra)。自反多面体是内部只有一个点,且距离这个点的所有边的距离是1的多面体。有一个假说是说在任何维度里,自反多面体的数量是有限的(up to SL(N;Z))。这个假说在1890年在二维空间里被证明是正确的,这样的多面体只有16个;100多年后,这个假说才在三维空间里被证明是正确,且是用当时算力最大的计算机花了一年时间才算出来这个数字(4130)。而到四维空间,这个数字就增长到了4.7亿多。对于四维以上的空间,这个假说还是一个开放问题。从这个例子我们可以看到,为什么一个数学物理问题使我们考虑到一个代数几何问题,然后这个代数几何问题又使我们考虑到一个组合几何问题。然而一旦进入组合数学的世界,你就会发现这些数字增长得非常快。
2017年,何杨辉老师开始思考是否可以用机器学习去理解几何,于是启动了一系列的超弦会议 String Data
He, Yang-Hui. “Machine-learning the string landscape.” Physics Letters B 774 (2017): 564-568.
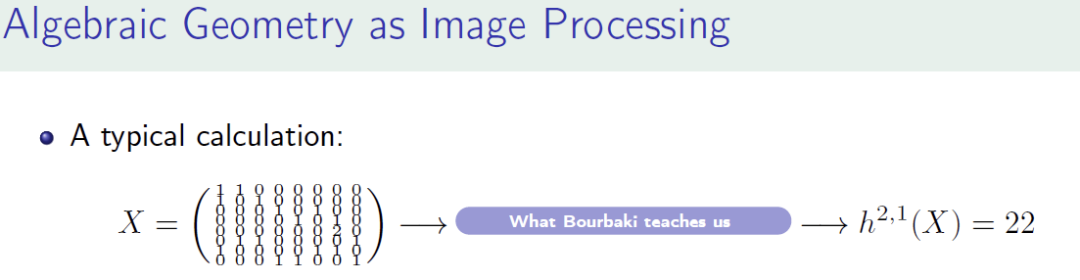
最常见的计算问题:计算一个流形或者代数簇的拓扑不变量。Bourbaki 告诉我们用同调去拼命计算。

总的来说,数学上有一套成熟的方法来计算这些拓扑不变量。然而,这套方法需要先将代数簇变成 Gröbner basis,而变换算法的复杂度是双指数(double exponential)的。如果所有的方程都是线性的话,那 Gröbner basis 变换就会变成一个普通的高斯 reduction,高斯 reduction 的复杂度是多项式的。但一旦进入非线性世界,复杂度就会是双指数时间。这套算法已经被编程到 Sage Math,M2 这些软件里了。对于简单的代数簇,可以用这套算法。但是只要代数簇稍变复杂,比如嵌入到两个或者三个射影空间的乘积,那目前任何计算机都无法算出来。比如如果你想做一个五次方程在四维的复射影空间(cp4)里面,也就是很有名的卡拉比丘流形,在这里面去算 Betti 数?用Sage Math可以算出来。但是如果你想做两个方程在五个或者七个复射影空间里面的话,用Sage Math就没办法算出来了。
何教授对此类问题有这样的洞见:是不是可以把十万个如图中X这样的代数簇(输入)和它们的 Betti 数(输出)作为一个简单的前馈网络(feedforward network)的训练数据,然后看神经网络的表现如何?
令人惊喜的是,神经网络的精确度很快就能达到很高。然后,最近有一批人用卷积神经网络和 Google 的 inception network 把精确度提高到了99.9%。这个实验告诉我们,代数几何有足够好的结构,使得我们能用简单的神经网络来找到它的内在规律。受到神经网络在代数几何领域的启发,2020-2021年期间,何教授和合作者写了一篇综述,来细数各个数学分支里可能用人工智能去找类似规律的问题。
举一个简单的例子:给出一个数列,推测下一个数字是什么。下面三个数列,人眼或许就能发现第一个和第二个数列的规律,第三个数列(Liouville Lambda函数,一个正整数的质因数个数是奇数还是偶数)用人眼可能很难看出来。神经网络能很好地发现这些数列的规律,对下一个数字做精确的预测吗?
对此,何教授做了一个实验,创建了对一个二元向量做二元分类的任务。比如,如果用0和1来表示一个正整数是不是素数,这样就能获得一个无穷的二元数列,然后尝试用监督学习预测下一个正整数是否是素数。训练集是这样组成的,用长度为100的 sliding window 从头开始滑动,每一个 window 里面的100个数作为输入,下一个数作为输出。然后,取5万个样本,把这些数据做20-80的交叉验证,用支持向量机、朴素贝叶斯、最近邻、前馈网络等模型进行训练,用准确率和 f-score 作为评估指标。
结果是这样的,对于第一个数列,任何一个分类器都能在几秒钟之内达到100%的准确率和 f-score。第二个数列涉及到素数的分布不均匀问题,因为素数是按照 x/log(x) 这样分布的,所以到后面会有越来越多的0,需要把窗户按比例拉长。这样处理之后,神经网络和支持向量机能达到80%的准确率和0.6的 f-score。但第三个数列,也就是 Liouville Lambda 函数(这是个非常深奥的数论问题,这个函数的表达跟黎曼猜想是等效的,知道这个就能解决黎曼猜想了),任何模型能达到的最高预测准确率也只有50%,跟投硬币的概率一样。
He, Yang-Hui. “Machine-learning mathematical structures.” International Journal of Data Science in the Mathematical Sciences 1.01 (2023): 23-47.
罗素-怀特海(Russel-Whitehead)的《数学原理》 (Principia Mathematica,1910s)将数学形式化、公理化。然而1930年代的时候,哥德尔用不完备理论(incompleteness theorem),图灵用不可判定性(undecidability)指出了这个框架的缺陷。
但务实的数学家基本不会考虑哥德尔的不完备理论,所以自动定理证明(automated theorem proving)仍广泛被数学家所接受。自动定理证明目前最成功的就是2013年开始的 Lean。帝国理工大学的Buzzard和Davenport已经把截至本科数学的所有命题和它们的证明过程用 Lean 跑过一遍,发现所有的命题都互相不矛盾。Buzzard认为数学研究的未来必须依赖自动定理证明,但可能需要一个世纪以上的时间才能实现。而Szegedy认为2030年应该就能用深度神经网络实现。我们把这种做数学的方式叫做“自下而上”的数学。
Lean 项目:https://lean-lang.org/about/
相关科普文章:https://www.quantamagazine.org/building-the-mathematical-library-of-the-future-20201001/
历史上,做数学研究的方式更接近于自上而下,也就是依靠直觉。一般是先看数据,通过对数据的观察得到猜想,然后再去验算或者证明,最后发表文章。数学家和理论物理学家写文章的过程跟思路正好相反,文章是从定义开始,到引理,然后定理等等,但做数学的过程是先想到一个例子,然后去做这个例子,接着做第二个例子、第三个例子,也许是对的,就做一个推想,然后写文章。
举个例子,18到19世纪最伟大的神经网络是高斯的大脑。在高斯16岁的时候就已经看出来小于x的质数的个数是x/log(x)。而人类直到50年后发明了复分析才能证明这个问题。所以他的直觉是一种超人的神经网络。虽然我们现在没有高斯的大脑,但我们有上千万个神经网络,来近似高斯的直觉感。再比如,20世纪 Birch 和 Swinnerton 提出的 Birch & Swinnerton-Dyer (BSD) 猜想(目前还是个开放问题),是由他们在剑桥的牛顿研究所(Issac Newton Institute)的地下室里通过计算很多很多的椭圆曲线的秩(rank)产生的。
一个有限群是完全由它的Cayley表定义的。那单群的Cayley表跟非单群的Cayley表是不是不一样呢?当时何老师及他的合作者取了大约一千个群,其中有的是单的有的是非单的。然后把这些群的 Cayley 表画在一个N平方的欧氏空间里,就得到很多很多点,再相加(因为up to commutation),就得到数十万的数据点,其中一些被标记为单群,另一些被标记为非单群。然后用支持向量机找出分离单群点与非单群点的超平面。这项工作只是一个proto conjecture,因为这样做可以得到这样的结果,但不知道为什么会得到这样的结果,而且不能告诉一个做表示论的数学家怎么去验证这个问题。未来他们希望能把这个做成一个明确的猜想。
He, Yang-Hui, and Minhyong Kim. “Learning algebraic structures: preliminary investigations.” International Journal of Data Science in the Mathematical Sciences 1.01 (2023): 3-22.
丘成桐先生在2020年曾问过何老师,如果取很多的有限图,能不能找到Ricci-平坦图形?他的灵感是卡拉比丘流形是平坦流形,那它是不是有一个离散领域的类比呢?何老师用了Wolfram 的有限 simple graphs 数据库,然后用分类或者回归或者卷积神经网络去学习这些图的邻接矩阵,看是否能找出 Hamilton cycle 或者 Euler cycle。其中 Hamilton cycle 是个NP问题,它是看一张图里面是不是能找到经过所有点并只经过一次的一条闭合路径。何老师发现从统计角度,神经网络找到有 Hamilton cycle 的图和没有 Hamilton cycle 的图,可以达到 80% 的准确率。
之前提到,用神经网络去预测下一个质数或者 Liouville Lamba 函数的规律都是很难实现的。也就是说,用人工智能的方法去硬算数论问题是很难的。但是,我们可以把数论问题变成一个椭圆曲线的问题。LMFDB 是一个包含1000万左右椭圆曲线的数据库。何老师与他的数论合作者曾尝试为给定的一个椭圆曲线算L-函数。椭圆曲线是一个二元三次多项式,目的是当系数为整数时,去找两个变量的整数解或者有理数解。很多数论问题都可以归根到这个问题上。目前没有办法找整数解,但可以定义一个生成函数然后在有限域上去数点,我们把这个生成函数叫做L-函数。
BSD 猜想告诉我们一个L-函数的解析性质,即椭圆曲线上的有理数点有多少。何老师不用椭圆曲线上面的系数,而是用L-函数上面的系数,用LMFDB数据库中的数据去验证。他发现用一些常用的机器学习算法去预测秩,torsion 等性质非常好。比如,对于判断椭圆的秩是0或是1 ,也就是它有有限多个有理数点还是无限多个无理数点,逻辑斯蒂回归很快就能达到几乎100%的预测准确率。(Goldfield 和 Bhargava 因为证明了椭圆曲线的秩从统计意义上来说有50%为0,50%为1,而获得了菲尔兹奖)
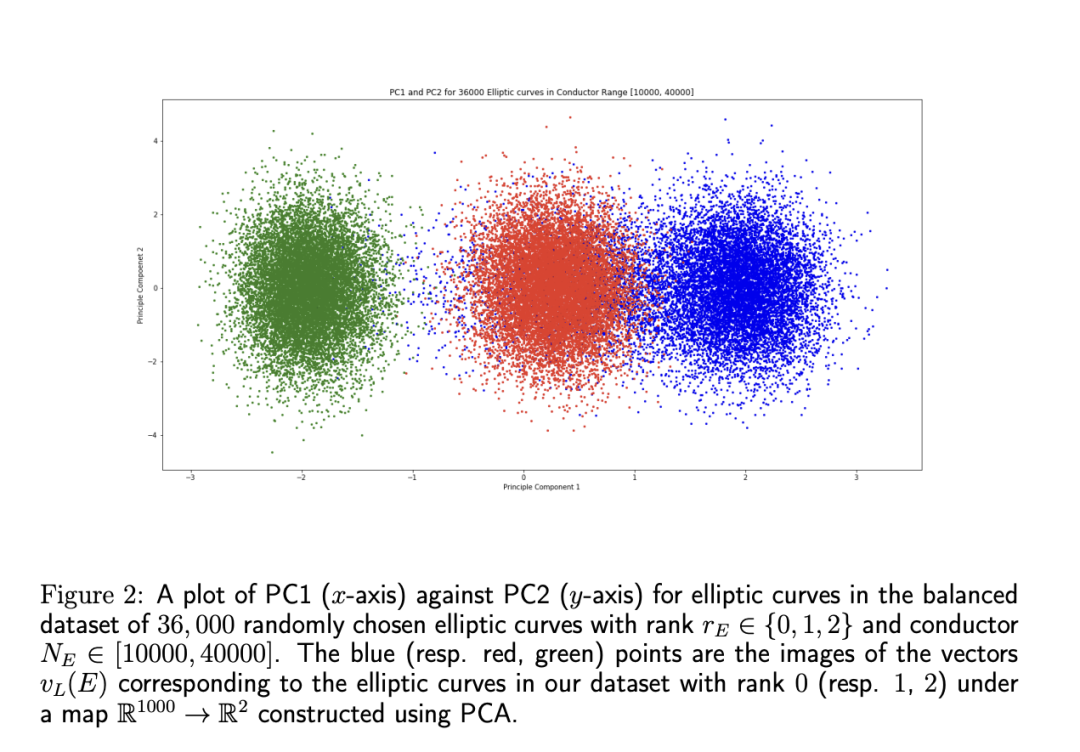
从这么多例子里,何老师想表达的主张是,如果你想去发现新的数学问题,就必须集合人和人工智能——需要人工智能来引导直觉,然后需要人来提出猜想。他提到了表示的重要性,比如他们之前用椭圆曲线的 Weierstrass 系数来预测BSD猜想的性质,得到的结果很不好,后面得到Oliver和Lee的启发用α(p)系数预测表现就很好。人的解读也很重要,比如通过解读用 α(p) 系数预测 BSD 猜想的性质的神经网络和主成分分析,得到了一个新的明确的猜想,他们把这个猜想叫做 Murmurations。他们想知道为什么机器学习能从α(p)系数很好地预测椭圆曲线的秩。通过主成分分析,他们发现秩为0、1和2的椭圆曲线的α(p)系数投射在二维空间上的点都是分离的,然后他们去进一步挖掘为什么这些点是分离的。
Alessandretti, Laura, Andrea Baronchelli, and Yang-Hui He. “Machine learning meets number theory: the data science of Birch–Swinnerton-Dyer.” MACHINE LEARNING: IN PURE MATHEMATICS AND THEORETICAL PHYSICS. 2023. 1-39.
He, Yang-Hui, et al. “Murmurations of elliptic curves.” arXiv preprint arXiv:2204.10140 (2022).
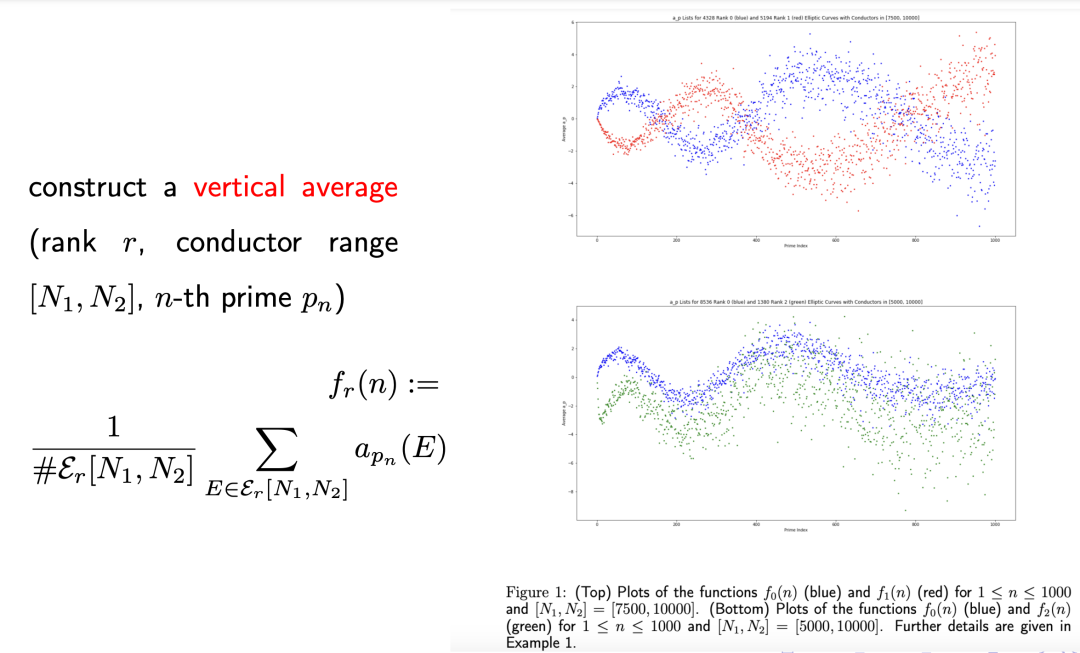
他们发现,PCA实际上是取了α(p)系数的 vertical 平均值(定义如下图左侧所示)。如果将这些 vertical 平均值画出来,会发现下图右侧这样的波动模式。
对于观察到的这个现象,最近何老师与许多做BSD猜想的研究者还在探讨中,目前得到了一些初步证明结果:波动在模型式里收敛到一个明确的曲线。而模型式和椭圆曲线有关,如果能证明出在椭圆曲线里也有这样的性质,而且能知道这个明确的曲线是多少,那对BSD猜想将会有一定的贡献。
2018年,何老师及合作者们取了Arxiv上大约200万篇涉及到五个领域(hep-th,hep-ph,gr-qc,数学物理学,hep-lat)的文章标题(word cloud见下图),然后用word2vec将标题语句中的文字基于上下文内容映射到一个向量空间。在这个由相近领域的文章标题组成的向量空间里,他们尝试去加减向量,找到了一些有实际意义的线性语法等式,比如弦理论+卡拉比丘流形=m理论+g2流形。他们相信,如果取完整的文章,然后把 LaTex 编辑的数学公式进行语言统一化,那就能做出一个数学的大语言模型。
He, Yang-Hui, Vishnu Jejjala, and Brent D. Nelson. “hep-th.” MACHINE LEARNING: IN PURE MATHEMATICS AND THEORETICAL PHYSICS. 2023. 223-291.
2019年,Tshitoyan 等人取了330万篇材料科学里的文章摘要作自然言语处理分析,结果不仅发现了元素周期表的结构,还发现了新的化学反应。因此,何老师希望也可以把数学里的文章下载下来,将文字规则化,看看能否发现新的数学猜想。
Tshitoyan, V., Dagdelen, J., Weston, L. et al. Unsupervised word embeddings capture latent knowledge from materials science literature. Nature 571, 95–98 (2019). https://doi.org/10.1038/s41586-019-1335-8
对于数学猜想的生成,从19世纪到21世纪,我们经历了三个阶段。19世纪是“高斯的眼睛”,20世纪 Birch + Swinnerton-Dyer 就需要用到计算机了,但21世纪光靠眼睛和简单的计算机实验已经不够了,而是需要人工智能引导人类直觉。所以数学的未来应该是下面三种运用人工智能方式的结合:
自下而上的自动定理证明,自上而下的机器辅助的人类直觉,以及数学的大语言模型。

何杨辉,本科就读于普林斯顿大学,以最优异的成绩获得物理学学士学位、应用数学证书和工程学证书(最高荣誉,Phi-Beta-Kappa)。随后,他又以优异成绩获得剑桥大学高等数学证书(Tripos)。之后,他在麻省理工学院获得理论和数学物理学博士学位。何杨辉继续在宾夕法尼亚大学从事博士后工作,之后作为 FitzJames 数学研究员和英国 STFC 理论物理高级研究员加入牛津大学。何杨辉在2010年加入伦敦大学城市学院,担任Reader。他目前是数学教授。他同时担任中国南开大学长江讲座教授,并自 2005 年起担任牛津默顿学院的导师和讲师。在2021年,他成为伦敦数学科学研究所的院士。何杨辉教授是一位数学物理学家,研究几何学、数论和量子场论/弦论之间的接口。最近,他帮助将机器学习引入纯数学领域,利用人工智能帮助发现新模式并提出新猜想。
数学与人工智能读书会第一期视频回放已上线,欢迎感兴趣的朋友深入学习
https://pattern.swarma.org/study_group_issue/518
数十年来,人工智能的理论发展和技术实践一直与科学探索相伴而生,尤其在以大模型为代表的人工智能技术应用集中爆发的当下,人工智能正在加速物理、化学、生物等基础科学的革新,而这些学科也在反过来启发人工智能技术创新。在此过程中,数学作为兼具理论属性与工具属性的重要基础学科,与人工智能关系甚密,相辅相成。一方面,人工智能在解决数学领域的诸多工程问题、理论问题乃至圣杯难题上屡创记录。另一方面,数学持续为人工智能构筑理论基石并拓展其未来空间。这两个关键领域的交叉融合,正在揭开下个时代的科学之幕。
为了探索数学与人工智能深度融合的可能性,集智俱乐部联合同济大学特聘研究员陈小杨、清华大学交叉信息学院助理教授袁洋、南洋理工大学副教授夏克林三位老师,共同发起“人工智能与数学”读书会,希望从 AI for Math,Math for AI 两个方面深入探讨人工智能与数学的密切联系。本读书会是“AI+Science”主题读书会的第三季。读书会自9月15日开始,每周五晚20:00-22:00,预计持续时间8~10周。欢迎感兴趣的朋友报名参与!
详情请见:
人工智能与数学读书会启动:AI for Math,Math for AI