导语

上一篇推送了小世界网络的来源和现象，知道了小世界网络从何而来。今天主要来看看如何用代码构建小世界网络。内容来自集智百科，集智百科是复杂系统领域的百科全书，涵盖复杂系统领域的基本概念（持续完善中）。

我们正在组织撰写翻译相应的维基词条，并附上代码实现。想要自己创建词条，一起贡献知识的小伙伴们可以通过链接报名哦。点击「编辑」，做些改变，按下「保存」，你将影响世界！

构建小世界网络

小世界网络也可引入延时，这不仅会产生分形，而且在特定条件下，还会形成混沌，或者在动态网络中转变为混沌。

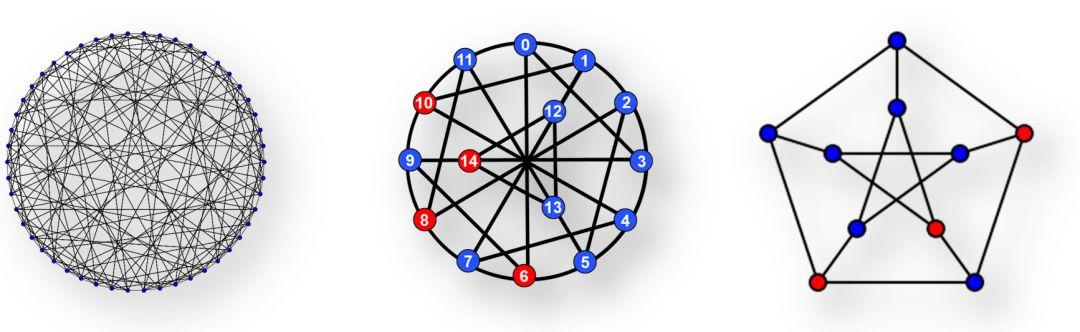
构造度直径图（Degree–diameter graph）

构造度直径图（Degree–diameter graph）的方法是：网络中每个顶点的邻居数量是有界的，而网络中从任意给定顶点到其他顶点（网络直径）是最小的。构建这样的小世界网络，其实是为寻找临近摩尔边界的图的秩，而做出的一部分努力。

Barmpoutis等人给出的从零开始构建小世界网络的另外一种方法，构建了一种平均距离极小且平均集聚度极高的网络。他们提到了一种复杂度恒定的快速算法，以及不同生成图鲁棒性的度量。根据每个网络的应用，可以从一个这样的“超小世界”网络开始，然后重新连接一些边，或者使用几个这样的小网络作为子图，构筑一个更大的图。

双相演化(dual-phase evolution)| 来源：https://www.google.com

通过双相演化(dual-phase evolution)过程，小世界属性可以在社交网络和其他现实世界系统中自然产生。在顶点之间的连接增长受到时间或空间的制约时，小世界网络尤其常见。该机制通常涉及相位之间的周期性变换，其中，在“全局”阶段——连接建立，而在“本地”阶段——连接被移除。

构建小世界网络代码实现

使用networkx生成小世界网络

详细代码如下：

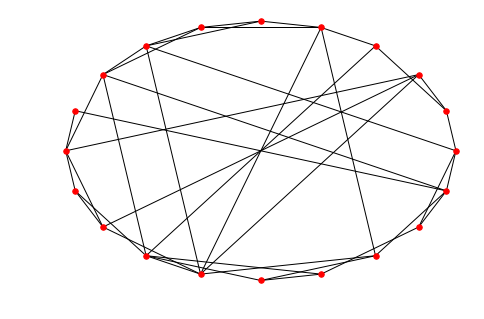
import networkx as nx

import matplotlib.pyplot as plt

# WS network

# 生成20个节点的小世界网络

# 每个节点有四个邻居

# 每条连边以0.3的概率随机重置链接

WS = nx.random_graphs.watts_strogatz_graph(20, 4, 0.3)

pos = nx.circular_layout(WS)

nx.draw(WS, pos, with_labels = False, node_size = 30)

plt.show()

此时得到的图片是下图所示:

使用原生方法x生成小世界网络

详细代码如下：

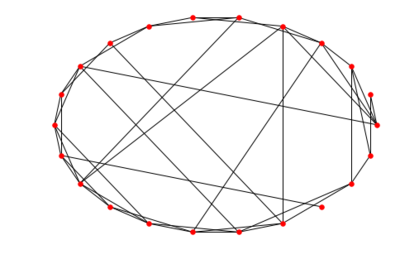
G = nx.Graph()node_num = 20neighbour_num = 4probility = 0.3# 节点与邻居相连for i in range(node_num):     from_node = i      for j in range(neighbour_num):         to_node = (i+j)% node_num - neighbour_num / 2         if to_node >= 0:             to_node += 1         G.add_edge(from_node,to_node)# 连边随机重连edges = copy.deepcopy(G.edges())for edge in edges:        if random.random() <  probility:         G.remove_edge(edge[0],edge[1])         ran_edge = np.random.randint(node_num,size=2).tolist()         G.add_edge(ran_edge[0],ran_edge[1])# 绘图pos = nx.circular_layout(G)nx.draw(G, pos, with_labels = False, node_size = 30)plt.show()

此时得到的图片如下图所示：

来源：集智百科

地址：

http://wiki.swarma.net/index.php/%E5%B0%8F%E4%B8%96%E7%95%8C%E7%BD%91%E7%BB%9C#.E4.BD.BF.E7.94.A8.E5.8E.9F.E7.94.9F.E6.96.B9.E6.B3.95x.E7.94.9F.E6.88.90.E5.B0.8F.E4.B8.96.E7.95.8C.E7.BD.91.E7.BB.9C

编辑：孟婕

推荐阅读

小世界网络之父邓肯·瓦茨经典回顾

小世界网络、偏好依附机制、跨学科研究

解读幂律与无标度网络 | 网络科学入门

无标度网络理论之父Barabási回应质疑

理论危机 | 无标度网络遭到史上最严重质疑

点击「编辑」，做些改变，按下「保存」，你将影响世界！

推荐课程