一项新的证明揭穿了一个阴谋，数学家曾担心它会像乌云一样盘旋在数轴之上。而在证明过程中，数学家们开发了另一套工具来理解算术的基本组成部分——质数。

在2021年3月发表的一篇论文中，德国哥廷根大学的 Harald Helfgott 和加州理工学院的 Maksym Radziwiłł 提出了一个改进的解决方案，以解决乔拉猜想（Chowla conjecture）的特定表述——这是一个关于整数之间关系的问题。该猜想预测，一个整数是有奇数还是偶数个质因数，并不影响它前后的整数是有奇数还是偶数个质因数。也就是说，相邻整数的某些最基本的算术属性不会有特定方式的关联。

这个看似简单的想法与数学中一些关于质数的最深刻问题交织在一起。加州大学洛杉矶分校的陶哲轩（Terence Tao）说，证明乔拉猜想是回答这些更棘手问题的“热身或者说垫脚石”。

然而几十年来，这样的热身问题本身就成了一项几乎不可能完成的任务。数学家们也是在短短几年以前才取得了一些小小进展，当时陶哲轩证明了这个问题的一个更简单的版本，称为对数乔拉猜想（logarithmic Chowla conjecture）。虽然他使用的技术被认为富有创新性且令人兴奋，但得到的结果不够精确，无法帮助在相关问题上取得更多进展，包括关于质数的问题。数学家希望还能有一个更强大、更普适的证明。

现在，Helfgott 和 Radziwiłł 提供了这样一个证明。他们的解决方案将图论（graph theory）技术直接推向数论（number theory）的核心，重新点燃了乔拉猜想兑现其承诺的希望——为数学家提供最终引导他们解决一些最难以捉摸问题所需要的想法。

1. 质数的阴谋

当数学家思考乘法和加法在质数方面的关系时，数论中许多最重要的问题就会出现。

质数本身是用乘法定义的：它们不能被除自身和 1 以外的任何数字整除；它们相乘则会构成其余的整数。但是几个世纪以来，涉及加法的质数问题一直困扰着数学家。例如，孪生质数猜想断言有无穷多个相差 2 的质数（如 11 和 13）。这个问题连接了乘法和加法两个通常相互独立的算术运算，因而具有挑战性。“这很困难，因为我们混合了两个世界，”布里斯托大学的 Oleksiy Klurman 说。

直觉告诉数学家，一个数加 2 应该完全改变它的乘法结构——这意味着一个数是否是质数（一种乘法性质）和两个单位之外的数是否是质数（一种加法性质）之间应该没有相关性。数论家没有发现任何证据表明存在这种相关性，但如果没有证明，他们也不能排除相关性出现的可能性。

“据我们所知，一个巨大的阴谋可能存在：每当一个数 n 决定成为质数时，它都会与邻居 n + 2 达成某种秘密协议，让它不再被允许成为质数”，陶哲轩说。

没有人接近排除这样的阴谋。这就是为什么在 1965 年，乔拉（Sarvadaman Chowla）制定了一种稍微简单的方法来思考邻近数字之间的关系。他想证明，一个整数是具有偶数或奇数个的质因数——这一条件被称为其质数数量的“奇偶性”（parity）——不应该以任何方式影响其相邻整数质因数的数量。

这个陈述通常用刘维尔函数（Liouville function）来理解，如果整数有奇数个质因数（如 12 = 2 × 2 × 3），则它为整数赋值 -1；如果整数有偶数个质因数（如 10 = 2 × 5），则它为整数赋值 +1。乔拉猜想预测，刘维尔函数的相邻取值之间应该没有相关性。

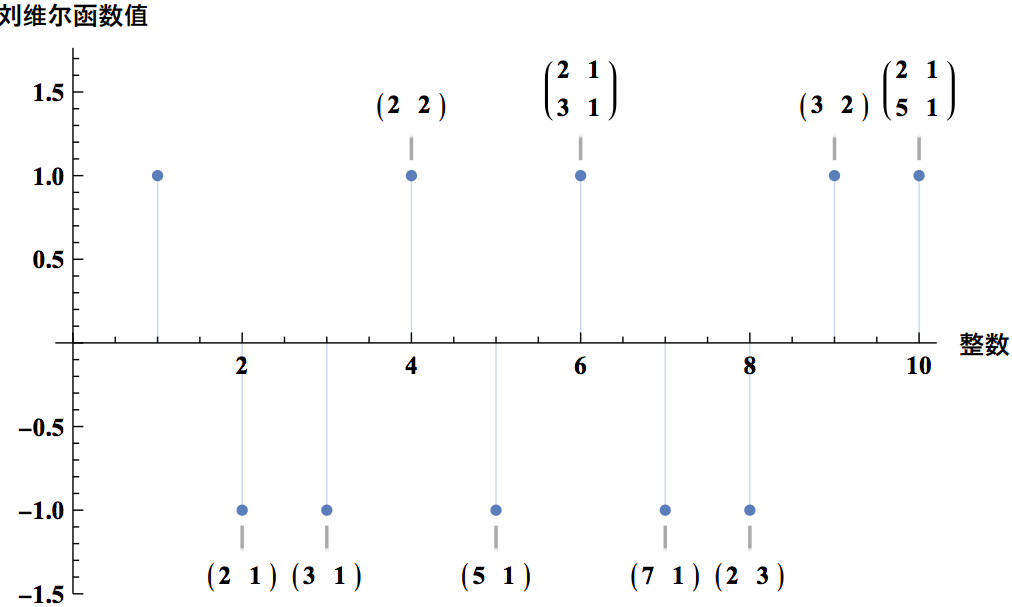
在探究奇偶性时，许多研究质数的最先进方法都失败了，而乔拉猜想正是要研究奇偶性问题。数学家希望通过解决这个问题，可以发展出新想法应用于诸如孪生质数猜想等问题。然而，多年来，它仍然只是一个幻想中的希望。不过，在 2015 年，一切开始改变。

2. 意外突破：奇偶簇烟消云散

芬兰图尔库大学的 Radziwiłł 和 Kaisa Matomäki 并没有着手解决乔拉猜想。相反，他们想研究刘维尔函数在一段短区间上的行为。他们已经知道，该函数的取值在整个正整数域上平均来看为 +1， -1各半；但它的值仍然有可能聚集在一起，在某个较长的连续区间内的取值要么全部为 +1，要么全部为 -1，从而形成团簇。

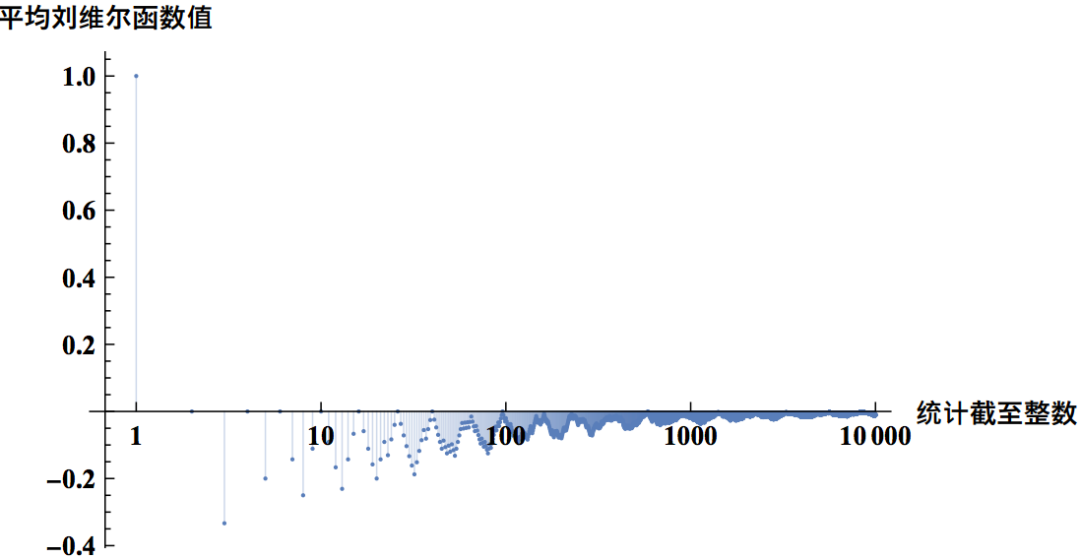
2015 年，Matomäki 和 Radziwiłł 证明这些团簇几乎从不出现。他们于次年发表的研究表明，如果选择一个随机数并查看它的成百上千个最近邻，大约一半整数的质因数数量是偶数，另一半是奇数。

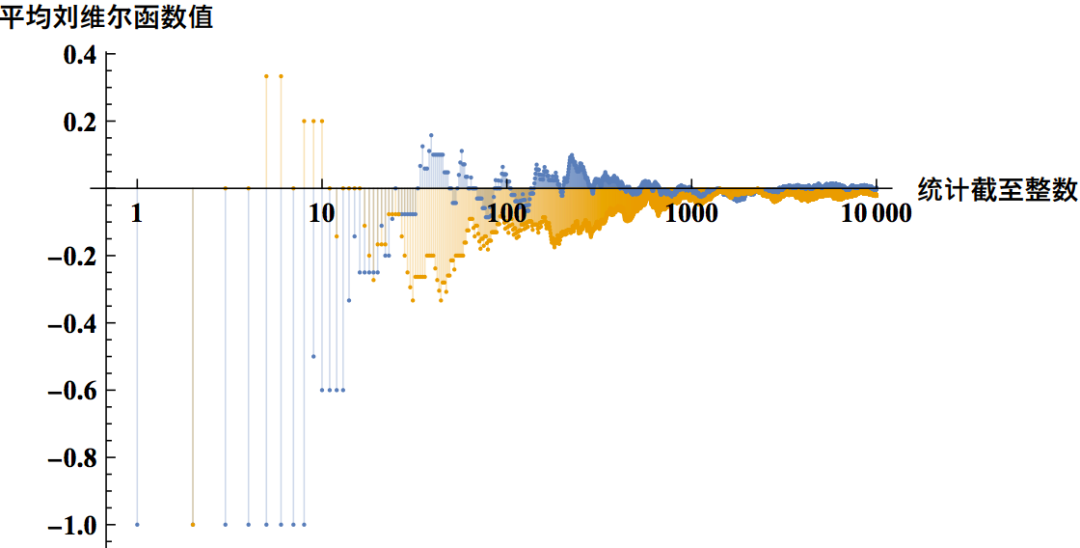
“这是拼图中缺少的重要部分，”蒙特利尔大学的 Andrew Granville 说。“他们取得了令人难以置信的突破，彻底改变了整个主题。”

这是一个强有力的证据，提示数字并不是上述大规模阴谋的同谋——不过，乔拉猜想是延伸到整个数轴的最高级别的阴谋。这就是陶哲轩进入的地方。几个月后，他发现一种方法可以在 Matomäki 和 Radziwiłł 工作的基础上解决一个更容易研究的问题，即对数乔拉猜想。在这个公式中，较小的数字被赋予较大的权重，以便与较大的整数一样被采样。

陶哲轩试图用反证法证明对数乔拉猜想。首先，他假设对数乔拉猜想是错误的——事实上，连续整数的质因数数量之间存在一个阴谋。然后他试图证明这样的阴谋可以被放大：乔拉猜想的一个例外不仅意味着连续整数之间的阴谋，而且意味着沿着整个数轴的更大阴谋。然后，他就能够利用 Radziwiłł 和 Matomäki 早先的结果，它恰好排除了这种更大的阴谋。乔拉猜想的反例会导致逻辑上的矛盾——从而证明反例不可能存在，猜想必须为真。

但在陶哲轩能做上述任何推理之前，他必须想出一种连接数字的新方法。

3. 图——连接数字

陶哲轩首先利用了刘维尔函数的一个定义特征。考虑数字 2 和 3，两者都有奇数个质因数，因此刘维尔值都为 -1。但因为刘维尔函数是乘法的，所以 2 和 3 的倍数也有相同的符号模式。

这个简单的事实具有重要的含义。如果2 和 3 都有奇数个质因数是由于某种秘密阴谋，那么 4 和 6 之间也存在阴谋——数字相差不是 1，而是相差 2。由此开始事情变得更糟：相邻整数之间的阴谋也意味着其所有倍数对之间的阴谋。“对于任何质数，这些阴谋都会随倍数放大而传播开来。”陶哲轩说。

为了更好地理解这个不断扩大的阴谋，陶哲轩从图的角度来思考它，图是由边连接的顶点的集合。在这个数字图中，每个顶点代表一个整数。如果两个数相差一个质数并且也能被该质数整除，则它们由一条边连接。

例如，考虑数字 1001，它可以被质数 7、11 和 13 整除。在陶哲轩的图中，它与 1008、1012 和 1014（通过一次加法）以及 994、990 和 988（通过一次减法）共享边。这些数字中的每一个依次连接到许多其他顶点。

总而言之，这些边编码了更广泛的影响网络：彼此连接的数字代表乔拉猜想的例外情况，其中一个整数的因式分解实际上确实会影响另一个的。

为了证明乔拉猜想的对数版本，陶哲轩需要证明这个图有太多连接，不能真实地表示刘维尔函数的值。用图论的语言来说，这意味着证明他的互连数字图是一个“扩展”图。

4. 拓展图上的随机游走

扩展图是衡量阴谋范围的理想标准。这是一种高度连通的图，尽管与顶点数量相比，边相对较少。这使得创建一个与图的其他部分没有太多交互的相互连接的顶点簇变得很困难。

如果陶哲轩能证明他的图是一个局部扩展图——图上的任何给定邻域都具有这个属性——他将证明对乔拉猜想的一次违背将传播到整个数轴上，这明显违反了 Matomäki 和 Radziwiłł 在2015年的结果。“获得相关性的唯一方法是，让整个群体都具有这种相关性。”陶哲轩说。

对一个图是否为扩展图的证明，通常可以转化为研究沿其边的随机游走。在随机游走中，连续的每一步都是偶然决定的，就像在城市中漫步，并在每个路口掷硬币来决定是左转还是右转。如果那个城市的街道形成一个扩展图，那么通过比较少的几步随机游走，就几乎可以到达任何地方。

但是在陶哲轩的图上游走是奇怪而迂回的。例如，不可能直接从 1001 跳到 1002，这需要至少经过另一个中间数。沿着这个图的随机游走从一个整数开始，加或减一个能够整除它的随机质数，然后移动到另一个整数。

重复这个过程几次并不明显能导向给定邻域中的任何点，但如果图真的是扩展图，情况应该是这样。事实上，当图上的整数变得足够大时，甚至连随机路径如何创建都不再清楚：将数字分解为它们的质因数，从而定义图的边，变得异常困难。“计算所有这些游走，会是一件可怕的事情。” Helfgott 说。

当陶哲轩试图证明他的图是一个扩展图时，“这有点太难了，”他说。不过他开发了一种新方法，基于熵这种对随机性的度量。这使他能够避免展示扩展图属性的需要——但需要付出代价。他可以解决对数乔拉猜想，但不如他想的那么精确。在猜想的理想证明中，整数之间的奇偶独立性应该总是很明显，即使沿着数轴的一小部分。但是在陶哲轩的证明中，直到采样了天文数字量级的整数，这种独立性才变得明朗。“量化来看，它不是很强大。”图尔库大学的 Joni Teräväinen 说。

此外，他的熵方法如何扩展到其它问题上仍然不清楚。牛津大学的 James Maynard 说，“陶哲轩的工作是一个彻底的突破，”但由于这些限制，“它不可能给出更多东西自然引导我们到问题的下一步，比如孪生质数猜想。”

五年后，Helfgott 和 Radziwiłł 设法做到了陶哲轩无法做到的事情——进一步扩大他发现的阴谋。

5. 朴素图帮助扩大阴谋

陶哲轩建立一个图的方法是，若两个整数相差一个质数并且可以被该质数整除，则在它们之间连一条边。而 Helfgott 和 Radziwiłł 考虑了一种新的“朴素”图（naïve graph），它抛弃了第二个条件，即只要两个整数相差一个质数，就可以建立一条连边。

直接结果是边的数量爆炸式增长。在这个朴素图上，整数 1001 与其他顶点的连接不是只有6个，而是有数百个。另一方面，这种图在一个关键方面却比陶哲轩的图简单得多：沿其边随机游走，不需要知道非常大整数的质因数。这两个方面共同作用，使得证明朴素图中的任何邻域都具有扩展属性变得更加容易——你很可能通过很少几步随机游走就能从一个顶点到达任何其他顶点。

Helfgott 和 Radziwiłł 需要证明这个朴素图逼近于陶哲轩的图。如果他们能证明这两个图是相似的，就可以通过研究朴素图来推断陶哲轩的图的属性。而且因为他们已经知道朴素图是局部扩展图，就可以推断陶哲轩的图也是（因此对数乔拉猜想为真）。

但是考虑到这个朴素图比陶哲轩的图的边多得多，如果存在相似之处，它也被掩埋了。“当你说这些图看起来很像时，这将意味着什么？” Helfgott 说。

6. 矩阵揭示隐藏的相似性

虽然这两种图在表面上看起来并不像，但 Helfgott 和 Radziwiłł 通过在两个视角之间转换来证明它们彼此逼近。一方面，他们将图视为图；另一方面，他们将图视为矩阵这种数学对象。

首先，他们将图表示为一个矩阵，这个矩阵是编码顶点之间是否有连边形成的数字阵列。然后他们从代表陶哲轩图的矩阵中减去代表朴素图的矩阵，结果是一个代表两者之间差异的矩阵。

Helfgott 和 Radziwiłł 需要证明，与该矩阵相关的特定参数（称为特征值）都很小。这是因为扩展图的一个定义特征是它的邻接矩阵具有一个大的特征值，而其余的则明显更小。如果陶哲轩的图和朴素图同样是扩展图，那么它也会有一个大的特征值——当从一个矩阵中减去另一个矩阵时，这两个大的特征值几乎会抵消，留下一组都很小的特征值。

但是特征值本身很难研究。相反，证明该矩阵的所有特征值都很小的等效方法又会回到图论。因此，Helfgott 和 Radziwiłł 将这个矩阵（代表他们的朴素图的矩阵与陶哲轩的更复杂的矩阵之间的差异）转换回了一个图。然后，他们证明这个图包含很少的会循环回到起点的随机游走（具有特定长度并且符合少数其他属性）。这意味着陶哲轩的图上的大多数随机游走基本上抵消了朴素扩展图上的随机游走——这意味着前者可以被后者逼近，因此两者都是扩展图。

7. 图帮助洞察隐秘结构

Helfgott 和 Radziwiłł 对对数乔拉猜想的解决方案标志着对陶哲轩结果的显著量化改进。他们可以对更少的整数进行采样就能得出相同的结果：一个整数的质因数数量的奇偶性与其邻居的奇偶性不相关。

牛津大学的 Ben Green 说：“这是解释质数和可除性看起来为何随机的一个非常有力的陈述。” 但这项工作可能更令人兴奋，因为它提供了“一种解决问题的自然方法” ，Matomäki 说——这正是陶哲轩六年前最初希望的直观方法。

扩展图之前已经在理论计算机科学、群论和其他数学领域带来了新发现。现在，Helfgott 和 Radziwiłł 也将它们用于数论问题。他们的工作表明，扩展图有能力揭示算术的一些最基本属性——消除潜在的阴谋，并开始解开加法和乘法之间复杂的相互纠缠。

Maynard 说：“突然之间，当使用图这种语言时，它会在问题中看到你事先无法真正看到的所有这些结构。这就是奥妙所在。”

参考资料

集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：

点击“阅读原文”，追踪复杂科学顶刊论文