PRL前沿：热力学稳定性意味着因果关系

导语

相对论流体力学理论的稳定性条件可以直接从平衡态时熵应最大化这一要求推导出来。1月6日发表在PRL上的一项最新研究用一个简单的几何论证证明，如果流体力学理论根据这个熵判据是稳定的，那么对平衡态的局部扰动不能传播到它们的未来光锥外。也就是说，在相对论流体力学中，非因果理论在热力学上必须是不稳定的，至少在接近平衡态如此。研究表明，稳定性和因果关系之间这种深层联系的物理根源在于熵和信息之间的关系。

研究领域：热力学，不可逆过程，非平衡态，相对论，信息论

梁金 | 作者

邓一雪 | 编辑

论文题目：

Thermodynamic Stability Implies Causality

论文链接：

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.010606

1. 热力学稳定性和因果，

彼此独立还是相互关联？

一个流体力学理论应该确保两个原理的有效性，即稳定性和因果关系。如果对全局热力学平衡态施加微小扰动，由此引起的偏差不会无限增长，而是随着时间推移保持有界，流体力学理论就被认为是稳定的；这源于随着时间趋于无穷，对耗散系统演化所至的平衡态的定义。另一方面，它要遵循因果关系，则需要信号的传播速度不超过光速；这源于相对论原理，如果信号是超光速的，在这个参照系中，结果将先于原因。

图1. 相对论中的光锥表示时空中事件的关系。假设因果过程的传播速度不超过光速，对于时空中的任意事件 O，过去光锥中的事件可以影响事件 O ，即如果发送一个物理信号可以抵达事件 O（左图）；未来光锥中的事件可以受到事件 O 的影响，即从事件 O发送的物理信号可以抵达这些事件（中图）。而光锥之外的类空（space-like）区域与事件 O 是没有因果关系的，因为信号无法以超过光速的速度传输（右图）。

一个新理论需要通过这两个检验，才会被认为是可靠的。到目前为止，研究中通常将这两个性质作为理论方程中不同的、没有联系的特征分开讨论。从直观上看，这种方法似乎很自然，因为稳定性和因果关系这两个原则分属于物理学的两个不同分支：热力学和场论。然而实际上，这两个特征是强烈关联的。此前的许多研究都表明，存在一种潜在的物理机制将稳定性和因果关系联系起来。

最近发表在 PRL 上的一篇论文提出了这样一个“完全解释性”的机制。研究人员证明：如果一个理论是热力学稳定的，即在平衡态时熵最大，那在平衡态附近，它也是遵循因果关系的。因果关系和稳定性之间的这种深刻联系源于熵和信息之间的潜在关系。

2. 几何证明：

热力学稳定性意味着因果关系

我们首先讨论热力学稳定性。在什么条件下，相对论流体是热力学稳定的？可以考虑流体“F”与热粒子浴“H”接触，假设整个“流体+热浴”系统是孤立的，并从状态1自发地演化到状态2。根据热力学第二定律，整个系统的熵不会减少：

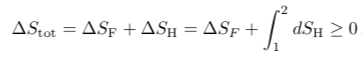（1）

流体 F 的平衡态是熵最大化的状态。对平衡态做任意微小扰动可以计算出，对于流体上的任意类空三维表面 Σ，需要满足

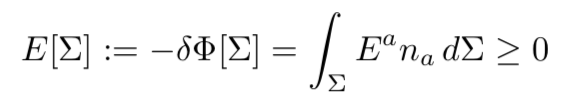（2）

公式的物理意义我们后面进一步探讨，重要的是由此可以得出三个热力学稳定性条件。作者们通过几何论证证明，满足这三个热力学稳定性条件就意味着，没有扰动可以传播到光锥之外，从而意味着遵循线性因果关系。

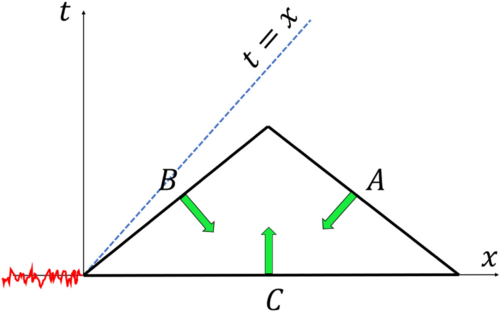
我们用 1+1 维惯性坐标系 (t,x) ，即一维时间+一维空间的情况作简单说明。如图2所示，三角形 ABC 的三条边都是类空的。考虑位于负半轴的初始扰动，结合三个热力学稳定性条件后，推导结果表明，扰动在三角形的三条边上都为0，即没有扰动可以传播到光锥之外 x>t 的类空区域。论文也给出了 3+1 维（三维空间+一维时间）推广的证明。

图2. 几何论证示意图。构建三角形 ABC，使其所有边都是类空的，边 B 和 C 相交于原点。绿色箭头是边的单位法向量的欧几里德表示，它们指向内侧。初始扰动（红色）位于原点左边，热力学稳定性条件意味着扰动被限制在 t≥x 的光锥内，从而意味着遵循因果关系。

3. 信息和熵之间的潜在关系

我们要如何理解热力学稳定性和因果关系之间的这种联系呢？一切源于熵和信息之间的潜在关系，这体现在由公式（2）得到的三个热力学稳定性条件中。

我们通常认为，熵意味着不确定性，也就是说，上述整个系统的熵 S_tot 反映了我们对系统微观态的认识的匮乏程度。根据玻耳兹曼方程，S_tot = klnW，W是给定宏观状态下所有可能的微观状态数量。从这个角度看来，公式（2）中 E 的物理意义是，

E =（平衡态的信息匮乏）-（扰动状态下的信息匮乏）

因此，E 是扰动所携带的净信息。吉布斯稳定性判据（E≥0）表明，任何扰动都会增加我们对微观状态的认识。

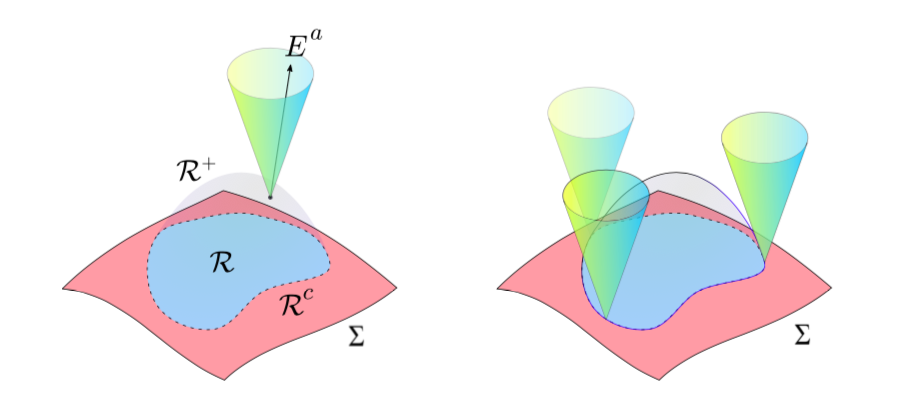
我们从这个信息论的角度来讨论三个热力学稳定性条件。条件（ii）是说：对于任意单位矢量 n_a，对每一个可观测量的扰动为0的任意点上，都有 E^an_a=0，并且仅在这些点上成立。结合条件（ii）可以确定，E^a 是扰动所传输的信息流（current of information）。

条件（iii）是：E^a的四维散度是非正的：∇_aE^a≤0。从信息论的角度来看，条件（iii）实际上就是热力学第二定律：我们关于系统微观状态的初始信息只能随着时间丢失（或从一个地方传输到另一个地方），但永远不会增加，因为当时间趋于无穷时，所有初始条件都趋向相同的最终宏观状态，即平衡态。

最有趣的是条件（i）：对于任意单位矢量 n_a，它是类时且指向过去的，都有 E^an_a≥0。它意味着在任何参考系下，信息密度是非负的，这等同于要求 E^a 是处在光锥之内且指向未来——正是这一点确立了因果关系。事实上，如果信息是通过非类空的四维信息流传输，它将沿着因果轨迹，不能离开光锥，也就是说没有任何扰动可以比光更快地传输信息。这个结果表明，信息不是在平衡区域自发形成的，不能从它的因果过去进入平衡态。

图3. 流体表面被分成平衡区域 R 和受扰动的区域 R^c。如果动力学是因果的，扰动不能传播到平衡区域 R 的未来（右图阴影区域）。事实上，在扰动传播到区域 R 之前，R 包含的流体无法“感知”到区域 R^c 偏离平衡态，它们“以为”整个流体处于全局热力学平衡态。

我们很自然会问相反的论证是否成立，因果关系是不是也意味着稳定性？一般来说，这个相反的论证是不成立的。单纯的因果关系通常并不意味着稳定性，只有在特定参考系中才可能证明稳定性。

这项研究工作表明，基于熵的稳定性判据也足以确保线性因果关系，这将简化对因果关系和稳定性的测试，有可能将其中一个约化为另一个。另一方面，研究揭示了信息论在相对论流体力学中的重要性。我们为何用了如此长时间才理解了这一点？作者们认为，原因可能是，此前的研究一直试图将因果关系与流体力学稳定性联系起来，而真正的联系是与热力学稳定性，这是一个更完整的可靠性判据。

因果科学读书会第三季启动

由智源社区、集智俱乐部联合举办的因果科学与Causal AI读书会第三季，将主要面向两类人群：如果你从事计算机相关方向研究，希望为不同领域引入新的计算方法，通过大数据、新算法得到新成果，可以通过读书会各个领域的核心因果问题介绍和论文推荐快速入手；如果你从事其他理工科或人文社科领域研究，也可以通过所属领域的因果研究综述介绍和研讨已有工作的示例代码，在自己的研究中快速开始尝试部署结合因果的算法。读书自2021年10月24日开始，每周日上午 10:00-12:00举办，持续时间预计 2-3 个月。