1963年,洛伦兹用蝴蝶效应形象地展现出了混沌的魅力:亚马逊热带雨林中的一只蝴蝶偶尔扇动几下翅膀,可以在两周以后引起美国得克萨斯州的一场龙卷风。正所谓“失之毫厘,谬以千里”,混沌理论告诉我们,即使人类掌握了确定性规则,依旧无法拥有预测未来的能力。本文从混沌的天气预测实验开始,介绍了混沌理论和实例:从分岔到分形,从树木、血管这些自然界的实例,到量子混沌再到人类的意识。
21世纪是复杂性的世纪,理解混沌是探索复杂性的关键环节。集智学园特别策划「混沌科学系列课程」,邀请9位从事混沌及相关跨学科研究的资深学者担任导师,导师团队由著名混沌理论学者、香港城市大学讲席教授、欧洲科学院院士陈关荣领衔。课程自2022年12月9日起,每周五晚在线授课。欢迎感兴趣的朋友加入,让我们一起进入混沌世界,探索不确定系统中的确定性规律!
Irfan Bashir, Hamid Rashid Shah | 作者
牛晓杰 | 译者
梁金 | 审校
邓一雪 | 编辑
1. 一个混沌理论的实验
2. 解释混沌理论:混沌科学
3. 什么是混沌理论?
4. 混沌斑图
5. 混沌理论举例
6. 量子混沌
在60年前一个寒冷的冬天,爱德华·洛伦兹正在他的电脑上进行一个天气模式模拟的实验。在输入了一些数字之后,他出去喝了杯咖啡。等到他10分钟后再次回来的时候,发现一些古怪的结果。由此他发现了后来著名的混沌理论——一个将永远改变科学的发现!
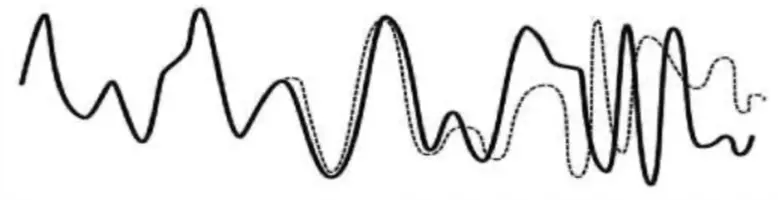
他的电脑模型是12个变量的组合,每一个变量代表天气的一个方面,诸如温度和风速。洛伦兹当时正在重复他之前的模拟。然而,当洛伦兹把他程序里的变量从0.506127四舍五入成0.506时,未来两个月的整个天气预测模式都完全改变了。在正常参数下,给定相同的起点,天气每次都会以相同的模式展开。而给定一个稍微不同的起点,天气应该以稍微不同的模式展开。四舍五入造成的误差肯定是微不足道的,它不应该造成什么大规模的影响。
在那个时期,科学的假设是,只要了解物理定律和系统的初始条件,就可以计算出一个封闭系统的大致行为。科学思维是,另一个星球上树叶的掉落不会影响到地球上台球的运动。人们相信,小的变化不会造成大的影响。法国数学家皮埃尔-西蒙·拉普拉斯(Pierre-Simon Laplace)在1814年出版的《概率哲学论文》(A Philosophical Essay on Probabilities)中说,如果我们知道宇宙目前的一切,那么“没有什么是不确定的,未来就像过去一样,会毫无保留的呈现在‘我们’眼前”。
但是,在洛伦兹的特殊微分方程系统中,随着时间的推移,小的错误会造成深不可测的变化。这些问题凝视着他,但他并没有答案。是否简单的模型可以产生显著的随机性?是否在一个系统中的简单模型会在另一个系统产生复杂性?是否随机性并不是模糊测量的副产品,而是一种常态?是否混沌并不是人类观察局限性的结果,而就是自然的底层法则?
这个出乎意料的结果使洛伦兹意识到,小的改变可以造成大的影响——这是对自然运转方式的强有力洞察。这个想法被称为“蝴蝶效应”。混沌效应或者蝴蝶效应就是用来表述“小的改变导致整个混沌系统重大变化”的观点。蝴蝶效应这个术语是洛伦兹提出的,他假设一只远处的蝴蝶拍打翅膀的行为可以引起一系列的复杂事件,最终导致其他地方的一场龙卷风。洛伦兹意识到,对初始条件的敏感性是导致非周期性行为的原因。这种效应后来获得了一个专有名词:初始条件依赖敏感性。然而,看一下民间传说就会发现,古代的诗人已经知道并回答了什么是混沌理论:
“因为少了一颗马蹄钉,而丢了一个马蹄铁。
因为丢了一个马蹄铁,而少了一匹战马。
因为少了一匹战马,而缺了一个骑兵。
因为缺了一个骑兵,而输了一场战役。
正如詹姆斯·格雷克(James Gleick)在他的书《混沌》(Chaos)中所说,“在混沌开始的地方,经典科学就止步了。只要世界上有物理学家在试图探究自然规律,TA就会在面对大气中的无序状态、动荡的海洋、野生动物种群的波动、心脏和大脑的振荡时感到特别的无知。自然界有其不规则、不连续和不稳定的一面。”
混沌科学孕育了自己的语言,包括分形、湍流、周期性、分岔、奇异吸引子、蝴蝶效应和敏感依赖等词汇。这些词代表了一个规则不同的世界——事物分支成奇怪的结构,遵循一种可以知道但不可能精确量化和预测的斑图和周期性。如果通过时空连续体的棱镜来参考,那么这个混沌世界的一切就好像是折回自身,同时成为未来和过去——它从自身汲取其周期性。混沌不是对秩序的拒绝,而是秩序的自然表达。
混沌科学似乎可以回答一些人类苦苦追寻的最基本问题。生命是如何开始的?什么是湍流?最重要的是,在一个创造更多无序的熵支配的宇宙中,秩序如何产生?以及古老的科学问题:微观世界如何将自己编织进宏观世界。孤立地研究一个原子或神经元时,其行为方式是一样的,但数十亿个原子和神经元的行为方式却完全不同。这是一门解开周期性和不可预测性之间联系的科学。
混沌的核心是对非线性的研究,这意味着玩游戏的行为有可能改变规则本身。非线性使得对非线性事物的理解变得困难,因为不同变量之间存在错综复杂的变化性,从而创造了丰富而复杂的行为。例如,人们不能给摩擦力定义一个恒定的重要性,因为它的重要性取决于速度,而速度又取决于摩擦力。因此,量化非线性就像解一个魔方,每次移动它时颜色都会改变。
过去两个世纪技术发生了重大变革,短期内的天气预测水平已经大大提升。但是长期天气预测仍然是棘手的问题。大部分现代天气预测模型,甚至是人工智能驱动的模型,都是通过分布在10-200公里范围内的地理监测点的网格进行预测。为了确定天气,气象学家使用一系列微分方程来分析原始数据,其中包括露水强度、温度、风、压力以及其他变量。但是地面站和卫星不能观察到所有的东西,因此对于一些起始数据,例如水分,必须通过猜测给定数值。大多数情况下,这种猜测是可靠的。
但是,假设我们能够将设备升级到足够精确的水平,并且用间隔仅几英尺的传感器覆盖整个地球;假设每个传感器都能给出气象学家想要观察的完全准确的读数;假设一台由人工智能驱动的量子计算机能够接收所有这些读数,并计算出以分钟为间隔的天气模式。那会发生什么?如果以上所有假设成立,我们是否能够绝对准确地预测天气?
我们将观察到的是,我们仍然无法预测特定地点或长期的天气模式。传感器之间的空间将隐藏微观波动——它一直延伸到量子范围,但是计算机并不知道。这些其实只是相比于平均水平的微小偏差。但在几分钟内,这些波动已经在几英尺外造成了微小的错误。很快,乘数效应(Multiplier Effect)将随之而来,错误将累计,甚至会扩展到10英尺的距离范围。因此,这使得人们不可能绝对准确地预测天气。
热液体是受混沌法则支配的许多流体力学过程之一。以一杯简单的咖啡为例,我们怎样才能计算出一杯咖啡究竟会以怎样的速度冷却下来?如果咖啡只是热的,它的热量会在没有任何流体力学运动的情况下耗散,因此不会产生湍流。但是如果温度上升到咖啡开始沸腾,会发生什么?
如果你仔细观察过一杯热咖啡,会立即注意到在饮料表面有一条暗线勾勒出的土灰色漩涡区域。这些旋转的斑图被称为对流单元。它标志着热咖啡上升到表面,而稍微冷却的咖啡被引力拉向底部的区域。对流是一种常见的过程,当较热的空气或液体位于较冷的下层时就会发生。这就是咖啡杯中发生的情况:上面的咖啡因蒸发而冷却,随着冷却也变得更重,被重力拉下底部。同时,底部的咖啡中较热的部分上升到顶部以取代它。
当较热的咖啡上升到顶部时,它的一小部分水蒸发了,然后在与表面上较冷的空气接触时凝结。这些水滴的大小和重量恰好能让它们留在表面。因此,在咖啡上面看起来像涂层的东西是小的云朵。水会反射光线,所以它们看起来是白色的。暗线部分是较冷的咖啡向底部沉降的地方。
漩涡可能很复杂。但最终我们能够知道这个系统会变成什么。随着热量的进一步消散,同时摩擦使移动的液体变慢,杯中咖啡的内部运动肯定会停止。洛伦兹在评论这一现象时曾说:”我们可能难以提前一分钟预测咖啡的温度,但提前一小时预测它应该没有什么困难。“
根据教科书上的对流模型,热的底部和冷的顶部之间的温度差控制着系统的流动。简单地说,热量向顶部移动,但并不干扰液体保持静止的趋势。
然而,当开始加热时可以观察到,随着液体变得更热,它的体积扩大,密度降低,使其轻到足以克服摩擦并向表面上升。但如果热量进一步增加,液体的行为会变得更加复杂。卷动的液体开始摇晃,为湍流的形成做准备。
因此,一个看似稳定的系统,当面对微小的变化时,如加热仅0.001度,就可以在几秒钟内从有序对流过渡到湍流混沌——即使这种系统是确定性的,它的最终结果可以预测。然而,在短期内,系统的确定性趋势必须向混沌让步,使得诸如“一杯咖啡的温度”这样简单的事情无法预测。这样的系统被称为遵循确定性的混沌,其行为原则上是可以被预测的,但“随着时间的推移”或在更小的“时间”尺度,其不可预知性会出现。
视频:Logistic 映射
自然界中的混沌斑图就在我们身边。这些斑图包括但不限于流体中的分形和湍流,螺旋形或者二维曼德布洛特集合形,或像洋葱中的嵌套层那样普遍的事物。
自然界中的混沌是一项迷人的研究。从最小的雪花到庞大的星系,它的每一点、每个声音和景象都在诉说着自己的故事。这不禁令人着迷,因为它有如此多的层次可以探索!从由不同材料组成的建筑结构(如砖或玻璃)内的音乐回声,一直到诸如包含后代遗传信息 DNA 的细胞等更小的结构,混沌无处不在。
大自然是一幅用秩序和混沌的图案编织的毯子。让我们探索其中的一些斑图。
4.1 洛伦兹系统:混沌理论中的蝴蝶效应和奇异吸引子
在洛伦兹观察到天气模式对初始条件的敏感依赖后,他对混沌背后的数学产生了浓厚的兴趣,并由此发现了著名的洛伦兹方程。1963年3月,洛伦兹写道,他想引入求解确定性非周期流和有限幅度对流(确定性混沌)的常微分方程。洛伦兹发现,当将傅立叶级数应用于瑞利的对流方程时,除了三个变量外,其他变量都趋于零。这三个变量表现出不规则的、明显的非周期效应。他利用这些变量构建了一个基于地球大气二维表示的简单模型。
他提出了一组对流微分方程,并将其简化到极致。尽管洛伦兹系统没有完全模拟对流,但它能够抽象出现实世界中对流的一个特征:热流体上升并向四处流动的循环运动过程。
洛仑兹方程包含三个参数:σ, ρ, β。接下来,我们均假设这些参数都是正的。在下面所有的数值计算中,我们取 σ = 10.0, β = 8/3,ρ 是变量。这里 x、y、z 并不是指空间中的坐标。x代表平面上的对流翻转,y和z分别代表水平和垂直的温度变化。该模型的参数为σ,代表流体粘度与其热导率之比;ρ 代表大气平面顶部与底部的温差;β 代表平面的宽度与高度之比。
洛伦兹的电脑记录下三个变量的变化值:0-10-0;4-12-0;9-20-0;16-36-2;30-66-7;54-115-24;93-192-74。随着预设时间间隔的推移,这三个数字先上升后下降。洛伦兹用每组的 xyz 值作为坐标绘制数据图。这副图显示了当一个变量经历有限时间内的变化时,混沌系统如何随时间变化。过去对系统的传统预期是,它要么会稳定下来,进入一个稳态,速度和温度的变量将不再变化;要么可能会形成一个循环,进入一种周期性重复的行为模式。而这两者都没有在洛伦兹系统里出现。
这幅图形成了一种无限复杂的感觉,同时包含了混沌和秩序。它总是在一定的范围内运转,但与此同时,它从不重复自己曾经出现过的状态。生成的混沌系统可预测地朝着相空间中的吸引子移动——但出现的不是点或简单的环,而是奇异吸引子。奇异吸引子是混沌系统在特定相空间中的一种表现,但吸引子也存在于许多非混沌的动力系统中。
它的形状看起来像个三维的双螺旋,看起来像一只蝴蝶。因此被称为蝴蝶效应。
洛伦兹吸引子(蝴蝶效应)微分方程在 Java 中的示例实现:
int i = 0;
double x0, y0, z0, x1, y1, z1;
double h = 0.01, a = 10.0, b = 28.0, c = 8.0 / 3.0;
x0 = 0.1;
y0 = 0;
z0 = 0;
for (i = 0; i < N; i++) {
x1 = x0 + h * a * (y0 – x0);
y1 = y0 + h * (x0 * (b – z0) – y0);
z1 = z0 + h * (x0 * y0 – c * z0);
x0 = x1;
y0 = y1;
z0 = z1;
// Printing the coordinates
if (i > 100)
System.out.println(i + ” ” + x0 + ” ” + y0 + ” ” + z0);
}
洛伦兹微分方程组证明了混沌中隐藏着秩序。这种混沌本身并不能简化为随机性。混沌的核心终于可以被数学的诗意语言表达了。混沌背后的数学理论表明,宇宙是由复杂的系统控制的,这些系统同时产生了湍流和相干——无论是木星的大红斑还是物种种群。蝴蝶效应就是混沌的体现。
视频:费根鲍姆常数
混沌的数学表示确立了非线性的重要性,这一特性支配着大多数自然系统,包括种群数量的增加。例如,如果1000只大象的群体每年净增10个成员,那么种群数量的增加可以在图表上表示为一条直线。然而,一群小鼠如果每年增加一倍的种群数量,将有一个非线性的增长模式——该图可以表示为一条上升的曲线。十年后,由于增长的非线性特征,两个小鼠群体(一个有22只小鼠,另一个有20只小鼠)之间的差异将膨胀到2000多只。因此,非线性增长模式常常导致动物种群规模混乱地上升和下降。
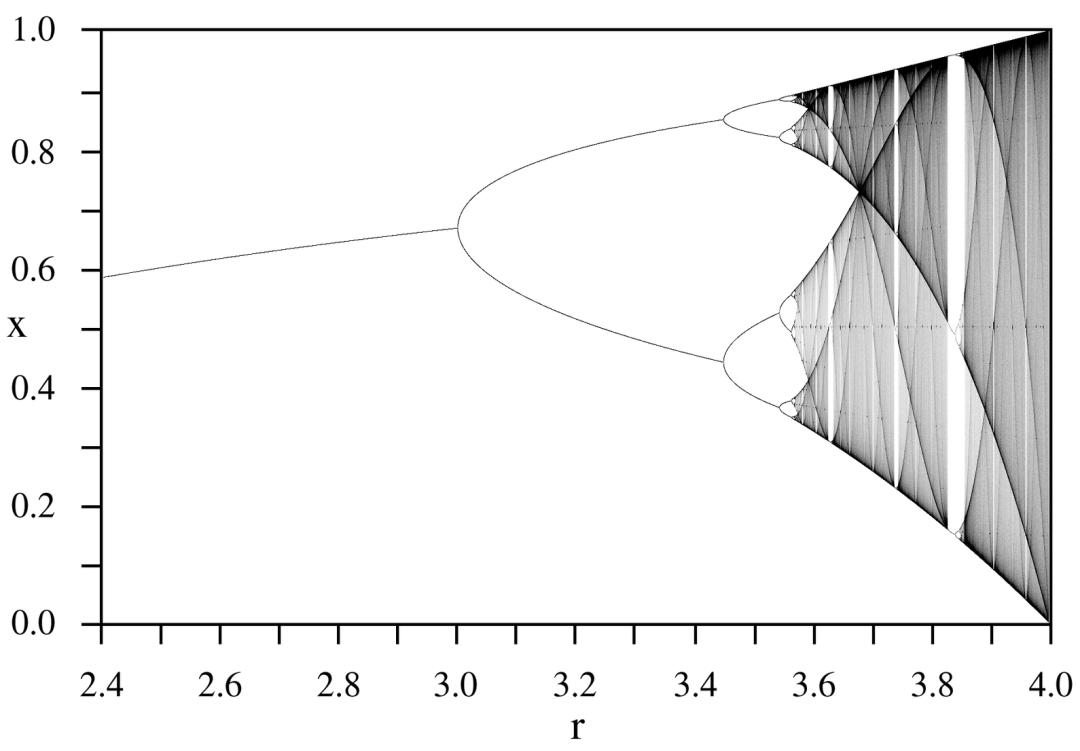
事实上,理解混沌理论最好的方法之一就是观察动物种群。假设方程 x_next = rx (1-x) 代表种群的增长。在这里,x_next 表示下一年的种群数量,x 表示现有年份的种群数量;r 表示增长率,(1-x)表示使增长保持在一定范围内的因素:当 x 增加时,(1-x) 下降。在这里,种群数量被表示为0到1之间的一个分数,其中0代表灭绝,1代表物种可能达到的最大种群数量。如果种群数量在一年内下降到某一水平以下,那么明年就有可能增加。但是,如果种群数量增长过快,物种内部对资源的竞争就会趋向于将其限制在一定范围内。
经过多次初始波动后,总体将达到平衡。当r值很小时,种群逐渐灭绝。对于较大的r值,总体可能收敛于单个值。对于更大的值,它可能在两个值之间波动,然后是四个值,以此类推。但对于更大的值,一切都变得不可预测。代表种群函数的线,最初是单一的,然后分裂成两个、四个…… 然后进入混沌。这种情况的种群数量-r曲线产生了有趣的结果。
当r在0和1之间时,种群最终灭绝。在 r = 1 到 r = 3 之间,种群数量收敛到单一值。在r = 3.2左右时,图分叉(分成两个),因为在r的这个值处,种群数量不收敛于单个值,而是在两个值之间波动。r值越大,分岔速度越快;在连续的周期翻倍之后,图像很快变得混沌。这意味着,对于r的相应值,种群数量在随机值之间不可预测地波动,从不表现出周期性行为。然而,仔细观察会发现,在混沌部分之间的某些点时,图会变得可预测。这些可以被称为“混沌中的秩序之窗”。在最初的混沌行为之后,混沌突然消失,留下一个稳定的三周期。然后继续加倍——6, 12, 24,再次进入混沌状态……图中的混沌行为实际上是分形的。它展示了在植物和动物种群调节的简单模型中固有的非线性如何导致混沌的行为。
超过某一点,周期性就会让位给混沌,波动根本就不会稳定下来。图中的整个区域都被完全遮住了。如果你继续观察一个由这种最简单的非线性方程组支配的动物种群,你会发现,复杂性被隐藏为随机性。然而,复杂性并不意味着随机性。对于动物种群数量的每一个疯狂的、不可控的变化,我们观察到有一连串的事件年复一年地出现。即使参数在上升,这意味着非线性推动系统越来越难,但会突然出现一个具有固定周期的窗口:一个奇数周期,如3或7。种群数量变化的模式在3年或7年的周期中重复出现。然后,周期加倍的分叉以更快的速度重新开始,迅速通过3、6、12……或7、14、28……的周期,然后再次中断,重新进入混沌。
放大后可以看到,上图中的混沌部分无休止地重复着同样的模式。分形是永无止境的。分形是无限复杂的斑图,在不同的尺度上具有自相似性。它们是通过在一个持续的反馈循环中不断重复一个简单的过程而产生的。从本质上讲,分形是一种永远重复的斑图,分形的每一部分,无论你如何放大,或缩小,它看起来都与整个图像非常相似。在递归的驱动下,分形是动态混沌系统的图像——它是混沌的图片。正如詹姆斯·格雷克(James Gleick)所说,”这是一种看待无限的方式”。
经过调查,数学家米歇尔·费根鲍姆(Mitchell Feigenbaum)发现,当他用每个分岔段的宽度除以下一个分岔段的宽度时,它们的比率会收敛到一个常数,被称为费根鲍姆常数,即4.6692016090。对于所有的分叉图,无论他使用什么函数,这个数字都是一样的。尺度是关键。费根鲍姆认为,(跨越不同范围的)尺度是理解湍流等复杂现象的关键。费根鲍姆提出了一种称为周期倍增的情况来描述规则动力学和混沌之间的转变。他的建议是基于1976年生物学家罗伯特·M·梅(Robert M. May)提出的 logistic 映射,梅在研究动物种群的繁荣与萧条模式时发现了分岔。
随着时间的推移,复杂性的规则也被证明是普遍的,并适用于所有的动力系统,不管它们的组成部分是什么。这种行为可以通过一个简单的系统观察到,比如水龙头滴水。最初,水会一滴一滴地落下。随着水流的加速,它会成对地滴落,以此类推,然后它遵循一种混沌的行为。这种类型的行为适用于无数的混沌系统——从滴水到异常复杂的曼德布洛特集合。混沌无处不在。
出生于波兰的法裔美国人伯努瓦·曼德布洛特(Benoit Mandelbrot)是一位对实用科学有广泛兴趣的博学者。现在人们对分形几何的兴趣很大部分是他的功劳。他展示了分形如何在数学和自然界中呈现。事实上,分形已经被用来描述经济、金融、股票市场、天文学和计算机科学的各种行为。他在分形几何学上的贡献为他赢得了“分形之父”的称号。
1961年,曼德布洛特在美国纽约州约克城高地托马斯·J·沃森研究中心担任研究科学家。作为一名尚未找到自己专业定位的年轻聪明学者,曼德布洛特正是那种IBM招聘时所渴求的特立独行的知识分子。招聘任务很简单:IBM参与了通过电话线传输计算机数据的工作,但一种白噪声不断干扰信息流,破坏信号。IBM希望曼德布洛特能对这个问题提供一个新的视角。
从孩提时代起,曼德布洛特就习惯在视觉层面思考问题,所以他没有使用现成的分析技术,而是本能地从白噪声产生的形状角度来研究它——这是IBM当今著名的数据可视化实践的早期形式。湍流的曲线图很快揭示了一个奇特的特征。无论图表的规模如何,无论它代表的是一天、一小时或一秒的数据,干扰的模式都惊人地相似。有一个更大的结构在起作用:一段时间的无误信号,紧接着就是一段时间的错误信号。曼德布洛特发现了误差爆发和清晰传输空间之间一致的几何关系。传输误差就像时间排列的康托集(Cantor set)。他将这种变化分为两种效应,他称之为“诺亚效应”(Noah Effect)和“约瑟效应”(Joseph Effect)。
诺亚效应意味着不连续性:当一个数量发生变化时,它几乎可以任意地快速变化。经济学家们传统上认为,价格的变化是平稳的——快速或缓慢,视情况而定。但平稳的意思是,它们在从一个点到另一个点的过程中经过了所有的中间水平。这种运动的概念是从物理学中借来的,就像应用于经济学的许多数学一样。但这是错误的。价格的变化可以是瞬间的跳跃,就像一条消息在电传电报上闪现和一千个股票经纪人可以改变他们的主意一样迅速。曼德布洛特认为,如果假定股票在从60美元跌至10美元过程中的某一时刻必须以50美元的价格出售,那么这条股市策略注定要失败。
约瑟效应意味着持续性。埃及遍地必来七个大丰年,随后又要来七个荒年。当然如果《圣经》用它来隐喻周期性的话是过于简化的。但洪水和干旱确实持续存在。尽管存在潜在的随机性,但一个地方遭受干旱的时间越长,它就越有可能遭受更长时间的干旱。此外,对尼罗河的数学分析表明,这种持久性持续了几个世纪,甚至几十年。诺亚效应和约瑟夫效应推动着不同的方向,但它们加起来就是:自然界的趋势是真实存在的,但它们来的快去的也快。
曼德布洛特后来将注意力转向测量海岸线。英国的海岸有多长?根据曼德布洛特的说法,答案取决于人们使用的尺子。据他说,海岸线无限长。一幅图画在他的脑海中形成,但它是朦胧的。微观世界和宏观世界之间有一种斑图联系。当从上面放大或缩小时,岩石海岸的粗糙程度看起来是一样的。曼德布洛特逐渐认识到,大自然倾向于在不同的测量维度上重复它的模式。
1945年,曼德布洛特的叔叔向他介绍了朱利亚(Julia)1918年的重要论文,认为这是一篇杰作,可以延伸出许多有趣的问题,但曼德布洛特并不喜欢它。事实上,他对他叔叔提出的建议十分抗拒,因为他觉得自己对数学的整个态度与他叔叔的态度是完全不同的。相反,曼德布洛特选择了属于他自己的非常不同的学术路线,然而,这条路线又让他回到了朱利亚的论文。
在加斯顿·朱利亚(Gaston Julia)和皮埃尔·法图(Pierre Fatou)之前的工作基础上,曼德布洛特使用计算机绘制朱利亚集的图像。通过研究这些朱利亚集的拓扑结构、棉花价格的模式、电子传输噪音的频率和河流洪水的重复,曼德布洛特认识到,自然系统中的不规则模式有一种自我相似性。存在一种跨越尺度的对称性——斑图中还有斑图。
曼德布洛特在加斯顿·朱利亚的工作基础上进行研究。朱利亚集分形通常是通过初始化一个复数 z = x + yi 产生的,其中x和y是图像像素坐标,范围约为-2至2。经过无数次的迭代,如果z小于2,我们就说这个像素是在朱利亚集里,并相应地给它上色。对整个像素网格进行这样的计算就可以得到一个分形图像。
曼德布洛特将c的值设置为 x + yi,其中x和y是图像坐标(也用于初始z值)。这就产生了曼德布洛特集合。曼德布洛特集合可以被认为是所有朱利亚集合的映射,因为它在每个位置使用不同的c,就好像在空间中从一个朱利亚集合转换到另一个朱利亚集合。结果是一个形状笨拙的虫子一样的结构,至少可以说,这是令人困惑的。更重要的是,每一个小版本都比上一个版本包含了更多复杂的细节。这些结构并不完全相同,但总体形状惊人地相似,只是细节不同。事实证明,这些细节的具体程度只受限于计算方程的机器的能力,而类似的形状可以永远持续下去——在无限的尺度上揭示越来越多的细节。这是一个确定的几何形状,它的粗糙度是有规则和参数的,但它是一种先前未被科学界所识别的几何形式。
曼德布洛特于1979年提出了曼德布洛特集。1982年,曼德布洛特在《自然界的分形几何》中扩展并更新了他的观点。在这本书中,曼德布洛特强调了自然界中许多分形物体的出现。他举的最基本的例子是一棵树。他指出,从树干到树枝等树的每个部分都非常相似,但也有细微的差异,这为整棵树的内部运作提供了越来越多的细节、复杂性和洞察力。忠实于他的学术根源,曼德布洛特基于这些自然实例提出了健全的数学理论和系统,他新创造的“分形几何”就是基于此。
分形斑图无处不在:在数学、工业、股票市场、气候科学、星系、树木,甚至在电影和游戏中也有分形的存在。事实上,多分形图案已经在量子领域被发现——在扫描隧道显微镜的原子级分辨率下,材料从金属向绝缘体的突变中,与单电子相关的波呈现了明显的多分形图案。让我们来看看我们在自然界发现的一些最令人惊讶的混沌模式。
木星的红斑是混沌研究中的一件艺术品。大红斑是木星南半球的一场风暴,它的红色云层以逆时针方向旋转,风速超过地球上的任何风暴。地球上的飓风是由水分凝结成雨时释放的热量驱动的,但红斑并不是。地球上的飓风以气旋方向旋转,在赤道上方逆时针旋转,在赤道下方顺时针旋转,就像所有地球上的风暴一样。相比之下,红斑的旋转是反气旋的。而且最重要的是,飓风在几天内就会消亡。但自1831年9月5日以来,人们一直能观察到大红斑。这个斑点是一个受湍流调节的自组织系统,混沌中稳定的矛盾组合创造了这个强大的风暴,这似乎没有尽头。
从主动脉到毛细血管,人体的血管形成了另一种连续体:它们分支,分裂,再分支,直到变得非常狭窄,以至于血细胞被迫单列移动。它们分支的本质是分形的。
肺是自然分形器官的一个极好的例子。一对人类肺的体积只有4-6升,但其表面积却能达到在50-100平方米。肺的表面积与容积比非常高,它对人体非常重要。是肺的分形结构使其具有这样的特征,从气管到分支顶端的肺泡一共有11个分支。分形分支几何提供了一种使非常大的表面积变得非常紧凑的方法。在这种情况下,身体里的每个细胞都必须非常靠近血管才能获得氧气和营养(100微米以内)。血管的分形分支系统可以达到直径约为8微米的程度,这也就是毛细血管的宽度。人体的血管长度可达15万公里左右,因为人体组织每毫米约有250个毛细血管,而毛细血管的平均长度约为600微米。
同样地,大脑的神经元也拥有分形模式。人脑由大约1000亿个神经元组成,这些神经元之间有大约100万亿个突触或连接,平均每个神经元可能要在同一时间与大约1000个细胞沟通。轴突伸出来与其他神经元的树突进行突触连接。正是神经元的轴突和树突的分形分支模式使它们能够与如此多的其他细胞交流。
事实上,癌症物质的分形维度要高于健康细胞的分形维度。乔治·华盛顿大学数学和工程系兼职教授艾伦·彭(Alan Penn)描述了他在这一领域的工作:核磁共振乳腺成像可能改善对400万名乳房X光检查无效的高危妇女的诊断。核磁共振成像的临床应用的困境是难以诊断哪些肿块是良性的,哪些是恶性的。研究的重点是开发强大的分形维度估计,这将改善良性和恶性乳房肿块之间的区分。
自然界中所有动物的身体结构都是分形的,它们的行为甚至时间也是分形的。我们的心跳看起来规律而有节奏,但当仔细观察计时结构时,就会发现它有非常轻微的分形。这非常重要:我们的心跳并不是规律的,而是有重要的微小变化。这种细微的变化大大减少了心脏的磨损。就像自相似树的树枝一样,健康人的心跳在统计上也是自相似的。此外,心脏病可以通过极端和无节奏的分形行为来检测。
分形图案在大自然中随处可见。树木是天然的分形斑图,这些斑图重复着越来越小的“复制品”,创造了森林的生物多样性。每根树枝,从树干到树梢,都是之前那根树枝的副本。这是一个基本原则,我们在自然界整个自然系统的有机生命形式的分形结构中会反复看到。
花朵、蕨类植物、树叶、河道、闪电、雪花是自然界分形的一些例子。Romanesco Broccoli 是花椰菜的变种,是一种极具分形的蔬菜。它的斑图是斐波那契数列或黄金螺旋的自然表示,这是一种对数螺旋,每四分之一转距离原点的距离都是黄金比例的一个因数。
斐波那契数列是自然界中常见而美丽的数字模式,它创造了黄金比例。蕨类植物是自相似集合的一个常见例子,这意味着它们的模式可以在任何放大或缩小的情况下用数学方法生成和复制。描述蕨类植物的数学公式以迈克尔·巴恩斯利(Michael Barnsley)的名字命名,是第一个表明混沌本质上不可预测、但通常遵循基于非线性迭代方程的确定性规则的数学公式之一。换句话说,使用Barnsley的蕨类公式反复生成的随机数最终产生了一个独特的蕨类形状的物体。许多植物在生成分枝形状和叶型时遵循简单的递归公式。
河流三角洲在本质上也趋向于分形;即使在天空中,基于卫星图片的分析也表明,从数百英里外观测到的云具有不变的分形维数;闪电不是直线传播的,而是遵循混沌的行为。闪电可以非常大,跨越数英里,但它在微秒内就可以形成;雷声是分形的声音,是由空气过热引起的。因为闪电的路径在3D空间中是一个锯齿形的分形,它到达我们耳朵所需的时间是不同的,因此我们听到的声音是一个分形模式。
星系是已知的最大的螺旋分形中例子。一个螺旋星系可能包含一万亿颗恒星。旋臂并不包含更多的恒星,但是,旋臂仍然更亮,因为它们包含许多由恒星形成的旋转螺旋波形成的生命短暂的极亮恒星。恒星形成的波之所以可见,是因为它们包含许多年轻的、非常明亮的恒星,它们的寿命很短,可能只有1000万年,而相比之下,更常见的恒星,如我们的太阳,寿命可达数十亿年。
量子混沌描述并试图理解原子和分子中电子的波状运动的本质(量子力学),以及电磁波和声学等。在一定程度上,这些波就像经典力学中粒子的混沌轨迹,包括光学仪器中的光线和复杂容器中的声波。量子混沌的研究包括动力学系统理论在量子体系中的应用。
“我们在日常生活中所经历的宏观世界是如何从肉眼看不见的微观世界中显现出来的?”这个问题,和科学本身一样古老。在过去的100年里,理解支配“宏观世界的经典力学是如何从支配微观世界的量子力学中衍生出来的”这一命题变得越来越重要。虽然科学界已经取得了巨大的进步,但仍然存在许多令人困惑的问题。混沌的出现很可能是量子世界和现实世界之间的共同连接。
量子混沌研究的核心目标是描述量子系统的普遍特性,这些特性反映了基础经典动力学的规则或混沌特征。研究人员已经观察到,经典混沌的后一种普遍属性与量子混沌的普遍光谱波动特征密切相关。
量子混沌最初是试图在量子力学系统中找到混沌,即对初始条件变化的极端敏感性。这一尝试失败了,因为人们最终意识到,这种敏感性并不存在。然而,在此过程中,人们发现混沌(或缺乏混沌)以其他方式反映在量子系统中。
量子混沌的一个迷人特征是,它揭示了非常不同的物理系统在行为上的大量普遍性。例如,在强多重散射问题中发现的声波强度、被称为瑞利分布(Rayleigh)的概率密度、中子从中重核散射的截面中的埃里克森波动、以及在混沌或无序的量子点中发现的电导率波动,都可以被视为拥有一个共同的基本统计结构。因此,人们能够看到系统之间的基本相似之处,否则这些往往会被忽略。普遍性意味着对一个系统的统计特性的许多方面缺乏敏感性,即缺乏某些种类的信息。此外,量子混沌把许多不相干的、看似不相干的概念,即经典混沌、半经典物理学和渐进方法、随机矩阵组合、路径积分、量子场论、安德森局域性,以意想不到的方式联系起来。
因此,看到量子混沌在许多领域的应用就不足为奇了。这些领域包括:(1)中核和重核中的低能质子和中子共振;(2)弹道量子点;(3)介观无序电子导体;(4)非阿贝尔规范场背景下的Dirac谱;(5)原子和分子光谱;(6)里德堡原子与分子;(7)微波驱动原子;(8)超冷原子和光学晶格;(9)光学谐振器;(10)晶体中的声学和在海洋中远距离传播的声学;(11)黎曼ζ函数和广义L-函数;(12)退相干性和保真度研究。还有很多其他的例子。
意识是一种涌现属性。正如神经科学家 David Eagleman 在他的书《大脑:你的故事》中解释的那样,观察意识最合适的方式不是关注各个部分,而是关注各个部分之间的相互作用。人类大脑中数百万个神经元中的一个神经元本身就足够简单。它以一种完美的、可预测的方式执行其功能,即神经递质通过突触发送信号。通过观察单个神经元来理解作为一个系统的意识是不可能的。重要的是神经元之间复杂的相互作用。每个神经元执行自己的简单功能;但是,在数百万个神经元之间的这种大规模的相互作用,产生了单个神经元无法解释的东西:意识。
我们可以说,意识与人类大脑中分布式互动的复杂性有关。人脑的功能结构本身就是一个分形反馈循环:分形大脑产生分形意识。人类的意识与中枢神经系统的电信号密切相关。如果大脑中没有电活动,你就会失去意识,甚至死亡。当意识出现时,大脑活动的熵会增加,而分形是高熵的,这也是一些研究人员认为我们的意识是分形的原因之一。其次,我们的中枢神经系统控制着我们身体和精神的大部分功能,它与分形有很多联系:第一,中枢神经系统的结构是分形的;第二,中枢神经系统的信号也是分形的。
视频:意识是分形的吗?
哲学家 Kerri Welch 通过时间和记忆的镜头,以更全面的方式看待意识。“我认为意识是一个时间上的分形。我们每时每刻都在接收无限多的数据,每次我们压缩处理这些数据的过程都是一次尺度上的飞跃。”Welch认为,感知时间不是一个线性的过程,而是一个“分层”过程,也就是一个分形。她认为这种“分形”会随着我们的变化而变化:例如,婴儿只生活在当下,不分割时间,肯定不会像成年人这般体验时间。这就是为什么对婴儿来说,大脑的δ波状态——类似于成年人在深度睡眠中看到的——占主导地位。随后,当我们成长到童年时期,我们开始看到更快的脑电波,θ脑电波……然后是α脑电波,最后是进入青春期后的β脑电波。这种对时间的分层理解与我们如何越来越多地将时间分割成越来越小的部分相对应。与此同时,“我们内部的密度也在增加。随着年龄的增长,我们会发生转变,接受周围的复杂性,并在内心重新创造它。我们内部的分形维数——即内部密度——正在增加。”
哈佛大学医学院的心脏病专家 Ary Goldberger 说得好:“我们本质上是分形的,这可能会导致你认为是我们将分形投射到世界上的,然后又看到它,并发现它很熟悉。”所以,当我们观察和创造艺术,当我们决定什么是高级艺术时,我们实际上只是在回看我们自己吗?创造在某种程度上是再创造吗?”
本文翻译自 projectnile.in.
文章题目:
The Mathematical Beauty of Patterns in Chaos Theory
https://projectnile.in/2021/06/06/quantifying-the-patterns-of-chaos/
1. https://www.popsci.com/story/science/predicting-weather-is-hard/
2. https://www.technologyreview.com/2011/02/22/196987/when-the-butterfly-effect-took-flight/
3. https://eapsweb.mit.edu/research/Lorenz/Deterministic_63.pdf
4. https://indianapublicmedia.org/amomentofscience/coffee-cup-convection.php
5. https://fs.blog/2017/08/the-butterfly-effect/
6. http://www2.me.rochester.edu/courses/ME406/webexamp5/loreq.pdf
7. http://links.uwaterloo.ca/pmath370w14/PMATH370/lorenz%20Latex.pdf
8. https://www.geeksforgeeks.org/creative-programming-processing-set-2-lorenz-attractor/
9. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3202497/
10. https://fractalfoundation.org/resources/what-are-fractals/
11. https://www.nature.com/articles/s42003-019-0715-9
12. https://iternal.us/what-is-a-fractal/
13. https://www.britannica.com/science/fractal
14. https://www.britannica.com/biography/Gaston-Maurice-Julia
15. https://www.api.simply.science/index.php/fractals-in-nature/10479-fractals-in-human-body
16. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5218578/
17. http://www.fractal.org/Life-Science-Technology/Publications/Fractals-and-Human-Biology.pdf
18. https://www.diygenius.com/fractals-in-nature/
19. https://cosmosmagazine.com/mathematics/fractals-in-nature/
20. https://www.ibm.com/ibm/history/ibm100/us/en/icons/fractal/
21. https://en.wikipedia.org/wiki/Benoit_Mandelbrot
22. https://mathshistory.st-andrews.ac.uk/Biographies/Mandelbrot/
23. https://www.treehugger.com/amazing-fractals-found-in-nature-4868776
24. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4005797/
25. https://nautil.us/issue/47/consciousness/is-consciousness-fractal
26. https://fractal.institute/encyclopedia/humanity/psychology/consciousness/
27. https://digitalcommons.ciis.edu/cgi/viewcontent.cgi?article=1043&context=cejournal
28. https://fractalenlightenment.com/18838/fractals/understanding-the-fractal-mind-and-fractal-consciousness
29. https://www.sciencedirect.com/science/article/abs/pii/S0169260718314263
30. https://ysjournal.com/chaos-theory-and-consciousness/
31. https://www.nasa.gov/image-feature/jpl/jupiter-s-great-red-spot-a-rose-by-any-other-name
32. https://www.amazon.in/Brain-David-Eagleman/dp/1782116613
33. https://www.amazon.in/Chaos-James-Gleick/dp/0749386061
34. https://fractalenlightenment.com/18838/fractals/understanding-the-fractal-mind-and-fractal-consciousness
35. https://fractal.institute/encyclopedia/humanity/psychology/consciousness/
36. https://nautil.us/issue/47/consciousness/is-consciousness-fractal
21世纪是复杂性的世纪,理解混沌是探索复杂性的关键环节。在科学、工程中,混沌与非线性方法已经成为研究动态系统的主要手段,加深了对气候、生态、大脑、流行病等诸多复杂系统问题的理解,并在湍流、加密、数据分析以及生命科学中有广泛应用。在社会、商业领域,混沌理论在通讯、交通、金融市场、疾病与信息传播等问题中亦有诸多启发和应用。随着混沌现象的进一步系统研究和广泛应用,它正在从一套理论发展为一门科学。
集智学园特别策划混沌科学系列课程,带领学员走近混沌理论,理解各类混沌系统,并尝试跨学科应用。课程邀请9位从事混沌及相关跨学科研究的资深学者担任导师,导师团队由著名混沌理论学者、香港城市大学讲席教授、欧洲科学院院士陈关荣领衔。课程自2022年12月9日起,每周五晚在线授课,学员群答疑交流。更有导师们梳理好的系列资料推荐。加入课程请扫海报中的二维码。
让我们一起进入混沌世界,探索不确定系统中的确定性规律!