从碰碰车谈起:拓展爱因斯坦关系,展示更多理论发现

导语
包景东 | 作者
论文题目: Generalized Einstein relation for aging processes 论文地址:
https://www.nature.com/articles/s42005-024-01791-7
布朗运动是广泛存在于自然界的一种随机现象,亦为许多学科普遍采用的模型。在物理上任何作为研究对象的系统,其必定不是孤立而是与它的环境发生互作用,那么,在粗粒化近似的层面上,人们就可以把环境对系统的影响以噪声来代替。毫不夸张地说,没有噪声或者涨落,化学反应无法发生,生命难以延续……
一、广义布朗运动
一、广义布朗运动
诺贝尔物理学家奖获得者费恩曼(R.P. Feynman 1918-1988)在《费恩曼物理学讲义·第1卷》中生动地描绘了布朗运动[1]。大概意思是:一个“保龄球”不慎落入了游乐场,它被碰碰车(图1)撞的不由自主地到处乱窜,同时碰碰车之间也相互碰撞。从远处看,保龄球的运动轨迹是连续但曲折的、不同时间段内具有自相似结构。当然,这种形象化的比喻隐含的要求还有:地面是光滑的、碰碰车本身应无操纵、其质量轻于保龄球,保龄球运动慢而碰碰车运动快。

费恩曼先生的这一逗,是否又对了呢?亦或说上述的类比会不会带来新物理?为了安全起见,每台碰碰车的圆周都装配上了软的橡皮带,因而碰碰车之间每发生一次碰撞,就会损失动能。长久地来观看,布朗粒子(保龄球)和周围的介质分子(碰碰车)都将停歇——称之为“老化”(aging),即有限寿命的布朗运动。近年来,颗粒物分子以及非理想双原子分子气体构成的媒介起到了众多碰碰车的作用。由于介质分子之间发生非弹性碰撞,分子的动能被转移到分子的内部势能而存储起来,因此分子的动能不断地减低,导致环境逐渐变冷(图2),身处其中的布朗粒子受到的阻碍也将随之变弱。
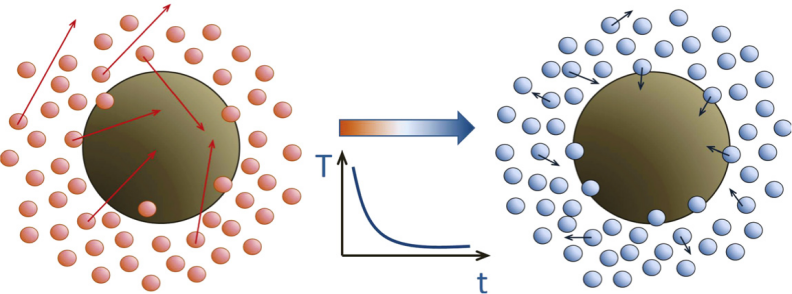
做随机运动的布朗粒子所受到的阻尼力和无规力来自同一起源,即周围介质分子对它的无规碰撞,故随机力(噪声)关联函数与阻尼核函数满足瞬间涨落耗散关系[2,3]。这里的阻尼强度和温度都可被假设成时间的幂律减函数,好处是由此所报告的系统速度关联函数(VCF)具有物理老化变量的特性:两时间以比的幂律形式而非差进入VCF之中[3],因而时间平移不变性遭到了破坏。这有别于传统布朗运动模型所给出的指数关联型VCF。所以说,费恩曼的“类比性、相关性、思想实验”[4]最为贴近科学与生活。
二、爱因斯坦关系
二、爱因斯坦关系
适用于布朗运动的爱因斯坦关系(Einstein relation,ER)将偏压粒子的平均位移与自由场中粒子的方均位移联系起来,但仅适合于平衡态或接近平衡态情况。一般地有:
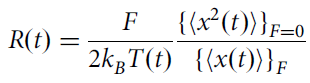 (1)
(1)
R(t)等于1即为原始爱因斯坦关系,不等于1称为广义爱因斯坦关系(GER)。式(1)看似简单,但它巧妙地将实验上难以测量的涨落量(分子)与容易确定的平均量(分母)联系起来。因为无外势作用下的布朗粒子轨迹是无规的,其离开原点位移的平均等于零,提供不了任何有用的信息,所以将每时刻粒子的坐标平方以表征扩散行为。而在偏压下粒子的运动是定向的,类似于沿着一个倾斜的滑梯(图3)做随机运动。从更深刻的意义上讲,爱因斯坦公式是后来久堡(Kubo)建立的第一和第二涨落耗散定理的前期准备。这是因为平均位移包含了摩擦强弱的作用,方均位移正比于涨落的大小,它们之间的关系等同于耗散与涨落两者之间的约束关系。

从常用的粒子位移与速度之间积分关系知,推广爱因斯坦关系到物理老化(physical aging)过程,可能打开一个新途径来审视它的重要性[3]。因为在式(1)中出现的平均位移包含了弛豫性,而方均位移包含着关联性。注意到粒子的平均位移,牛顿力学用的是“干”摩擦,即摩擦力正比于正压力,加速度正比于合力;朗之万随机动力学用到的是“湿”摩擦,即摩擦力正比于粒子的速度,加速度等于零。我们发现了一个介于两者之间的随机动力学——耗散加速度[3]或者力折合效应[5]。另外还报告了一种超慢扩散[3] :自由粒子方均位移以时间对数函数增长。
其实,爱因斯坦关系隐含着VCF这个核心要素。为了从新视角研究和连结近年来实验和理论的热点问题,即老化动力学、反常扩散以及遍历性破缺,推广ER到一般(特别是物理老化)情况下,将可探讨自旋玻璃、量子点、激光致冷原子以及颗粒物介质等系统的奇特现象。我们新近的工作[3]提出了一个瞬时涨落耗散关系约束下的惯性朗之万方程模型,由此解析给出以往需引入空间破缺才能有的标度律VCF。基于此解析推导出平均位移和方均位移表达式,通过引入一个修正因子R(t),进而得到GER,其包含了物理老化与时变温度效应。我们的广义爱因斯坦关系展示出三种结果[3]:式(1)中的R(t)的渐进值等于1、大于1和发散,分别对应于弹道扩散、超和欠扩散、指数超慢扩散,均显示系统与环境的非平衡性。
三、遍历性破缺
三、遍历性破缺
遍历性是平衡态统计物理的唯一假设,即一个观测量的时间平均等于它的系综平均。然而对于这个简单的表述,无论理论还是实验都难以直接证实,如同人们无法寻觅一个粒子是否访问了一个等能面上的所有地方(相格)那样,确定其满足了各态历经。

图4. 一个不光滑的等能面,就如同陆地上存在许多山丘和谷底。
如果一个等能面上存在无限深势阱或者无限高势垒(图4),那么粒子从某一初始位置出发,它将不可能访问所有的地方,称之为强遍历性破缺。另外的情形是,虽然等能面是光滑的,但是由于系统与其环境发生不彻底耗散,以致于系统对它的初始准备还保留着部分记忆,体现在观测量的关联函数渐进不为零,称之为弱遍历性破缺,系GER面临的挑战[3,6]。
迄今,一些遍历性条件被提出了,常见的有两个。其一,辛欣(Khinchin)定理,即观测量关联函数随着两时间差的增加而渐进消失。意味着系统当前的状态与其先前的准备无关,系统需要访问等能面上的所有地方。其二,把观测量的有限时间平均看作一个随机变量,计算它的方差。如果长时间后,这个方差等于零,就表示观测量的时间平均为一定值,而观测量的系综平均往往是在一个定态分布密度函数下求得的,应该也是一个常量。所以,观测量的时间平均趋于定常是遍历性成立的必要条件。作为GER的应用,我们讨论了遍历性弱破缺条件和非弹碰撞颗粒物介质中的布朗运动。发现辛欣(Khinchin)定理即VCF渐进消失以及观测量时间平均的分布收敛的条件,均不能保证时间平均等于系综平均。如所周知,理论上用系综平均,实验上用时间平均(即在一条轨迹上打卡记录)。后者是近年来发展起来的单粒子径迹技术[7],其重要性在于用较小的单轨迹代价来得知系综刻画的物性行为。
(5) 为使爱因斯坦关系得以应用,系统需经过一个有效遍历性时间的演化[7]。
*国家自然科学基金委员会理论物理专款“理论物理文化传播”资助项目(12347212)。
** jdbao@bnu.edu.cn
主要参考文献
[1] R. P. Feynman,R.B. Leighton,M. Sands著. 费恩曼物理学讲义•第1卷[M]. 上海科学技术出版社,2005.
[2] A. S. Bodrova, A. V. Chechkin, A. G. Cherstvy, and R. Metzler, Ultraslow scaled Brownian motion[J], New J. Phys. 17, 063038 (2015).
[3] J. D. Bao and X. R. Wang, Generalized Einstein relation for aging processes[J], Communications Physics 7,249 (2024). https://doi.org/10.1038/s42005-024-01791-7 “老化过程的广义爱因斯坦关系”.
[4] 包景东. 物含妙理——像费恩曼那样机智地教与学[M]. 清华大学出版社, 2018.
[5] J. D. Bao, Y. Z. Zhuo, F. A. Oliveira, and P. Hanggi, Intermediate dynamics between Newton and Langevin, Phys. Rev. E 74 , 061111 (2006). “牛顿和朗之万之间的动力学”
[6] J. D. Bao. Generalized Einstein relations and conditions for anomalous relaxation[J], Phys. Rev. E 100, 052149 (2019) “广义爱因斯坦关系和反常驰豫” .
[7] J. D. Bao, X. R. Wang, and W. M. Liu, Ergodic time scale and transitive dynamics in single-particle tracking[J], Phys. Rev. E 103, 032136 (2021). “遍历性时间尺度和单粒子径迹演变动力学”.
[8] J. D. Bao and Y. Z. Zhuo, Ballistic Diffusion Induced by a Thermal Brodband Noise, Phys. Rev. Lett. 91, 138104 (2003). “热宽带噪声诱发弹道扩散”
复杂系统自动建模读书会
“复杂世界,简单规则”。
集智俱乐部联合复旦大学智能复杂体系实验室青年研究员朱群喜、浙江大学百人计划研究员李樵风、清华大学电子工程系数据科学与智能实验室博士后研究员丁璟韬、美国东北大学物理系Albert-László Barabási指导的博士后高婷婷、北京大学博雅博士后曹文祺、复旦大学数学科学学院应用数学方向博士研究生赵伯林、北京师范大学系统科学学院博士研究生牟牧云,共同发起「复杂系统自动建模」读书会第二季。
读书会将于9月7日每周六晚上20:00-22:00进行,探讨四个核心模块:数据驱动的复杂系统建模、复杂网络结构推断、具有可解释性的复杂系统推断(动力学+网络结构)、应用-超材料设计和城市系统,通过重点讨论75篇经典、前沿的重要文献,从黑盒(数据驱动)到白盒(可解释性),逐步捕捉系统的“本质”规律,帮助大家更好的认识、理解、预测、控制、设计复杂系统,为相关领域的研究和应用提供洞见。欢迎感兴趣的朋友报名参与!
复杂系统自动建模读书会:从数据驱动到可解释性,探索系统内在规律|内附75篇领域必读文献
6. 加入集智,一起复杂!
点击“阅读原文”,报名读书会










