计算复杂性理论50年:从P与NP问题到元复杂性

导语
文章题目:Complexity Theory’s 50-Year Journey to the Limits of Knowledge
文章链接:https://www.quantamagazine.org/complexity-theorys-50-year-journey-to-the-limits-of-knowledge-20230817/
1. 起源
2. 障碍
3. 机遇

复杂性理论发展的100年历程。|来源:Samuel Velasco/Quanta Magazine
1. 起源
1. 起源
2007年秋季学期,Marco Carmosino 在读大二,正考虑从大学退学去设计电子游戏。开学第一周,他硬着头皮去参加马塞诸塞大学阿默斯特分校计算机科学专业必修的数学课。然后教授提出了一个改变他一生的简单问题:你怎么知道数学真的有用?
Carmosino 现在成为了IBM的理论计算机科学家,他回忆当时场景说,“这个问题让我坐直起来,并集中注意力”。他后来报名了一个关于库尔特·哥德尔(Kurt Gödel)工作的选修研讨会。哥德尔关于自指论证的工作令人眼花缭乱,既暴露了数学推理的局限性,还为未来所有关于计算基本极限的工作奠定了基础。Carmosino 从中受益匪浅。他说道:“我完全听不懂,但我知道这就是我想干的。”
如今,即使是经验丰富的研究人员在面对理论计算机科学中的核心开放问题——即P与NP问题——时,也会发现理解欠缺。这个问题本质上在问:那些长期以来被认为难以计算的问题是否可以(通过我们尚未发现的秘密捷径)轻松解决?或者,就像绝大多数研究者怀疑的那样,他们的确就是很难。关键在于可知事物的本质。
尽管研究者们在计算复杂性理论(computational complexity theory)——研究不同问题的本质困难——领域耕耘数十年,但P与NP问题仍让人摸不着头脑,甚至不知道证明该从何开始。Michael Sipser 是麻省理工学院资深复杂性理论学家,在20世纪80年代思考这个问题多年。他形容这种探索就像“没有路线图,走进荒野。”
证明计算问题难以解决本身似乎就很艰巨。但为什么这么难呢?到底难成什么样呢?Carmosino 和其他元复杂性(meta-complexity)子领域的研究者们将此类问题重新表述为计算问题,通过复杂性理论的视角观察复杂性理论本身来推动该领域向前发展。“你可能会想,‘好吧,这挺酷的。也许复杂性理论家们疯了。’” Rahul Ilango 如是说,他最近在该领域取得了一些令人兴奋的成果。
研究者们通过研究这些问题发现,证明计算难度的难度与一些看似无关的问题密切相关。在看似随机的数据中发现隐藏的模式有多难?如果真正的困难问题确实存在,那么它们究竟有多少?“很明显,元复杂性接近事物的核心。” Scott Aaronson 如是说,他是德克萨斯大学奥斯汀分校的复杂性理论学家。
从P与NP问题转变到元复杂性的路,研究者们走得漫长而曲折。旅程并不轻松,路上尽是错误的分岔和路障,且往复循环。然而,对于元复杂性的研究人员们来说,踏入未知的旅程本身就是奖励。加拿大西蒙·弗雷泽大学(Simon Fraser University)的复杂性理论家 Valentine Kabanets 说,从提出看似简单的问题开始,“行至何处,不知道。”
已知的未知
P与NP问题(P versus NP problem)的名称平平无奇,是因为复杂性理论学家习惯用暗示纳斯达克股票代码的标签将计算问题分类为广泛的“复杂性类别”。计算问题可以被算法(一连串精确的指令)解决。但不是所有的算法都同样有效,算法之间的差异暗示了不同类别问题之间的根本差别。复杂性理论学家面临的挑战就是,将这些“暗示线索”转化成在复杂性类别之间关系的严格定理。
Kabanets 说:“这些关系反映出的东西远超任何特定技术,是关于计算的永恒真理,就像发现宇宙法则一样。”
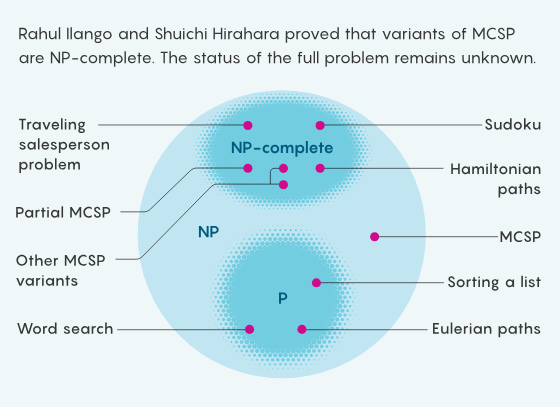
复杂性类别的数目不断增长,成百上千,“P”和“NP”是其中两个最重要的成员。简单来说,“P”是一类易于解决的问题,比如按字母顺序排序。“NP”类问题则易于验证解决方案,例如数独谜题。由于所有易于解决的问题都易于被验证,因此“P”类问题从属于“NP”类。但有些“NP”类问题看起来很难解决——如果没有预先尝试,你就不能立马凭直觉给出数独问题的答案。这种显见的困难是幻觉吗?——我们能否找到简单的技巧轻易解决所有“NP”类问题?
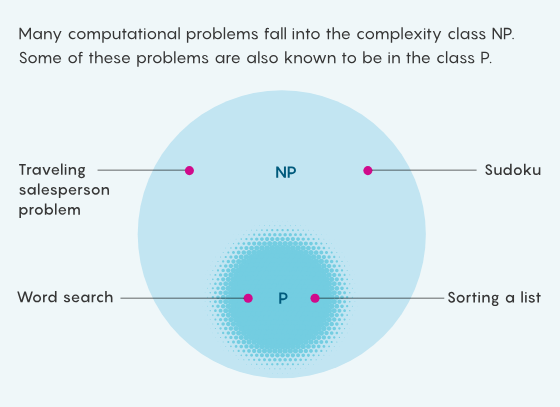
如果可以,那么 P=NP :这两个问题就是等价的。如果是这样的话,那么我们一定能找到某种方法轻易解决大量的数独谜题、轻易优化全球航运路线、破解最先进的密码以及自动化证明数学定理。如果 P ≠ NP,那么许多原则上可以解决的计算问题将永远无法解决。
在P与NP问题提出之前,实际上可以说是早在现代计算机科学开始之前,研究者们就担心形式数学推理(formal mathematical reasoning)的局限性。1921年,数学家戴维·希尔伯特(David Hilbert)抛出了一个研究计划,旨在确保数学的绝对确定性。他希望能从一些简单的假设(即公理,axioms)开始,导出一个符合三个关键条件的统一数学理论。
希尔伯特的第一个条件是一致性(consistency),这是数学体系不存在矛盾的基本条件:如果可以从同一个公理出发证明两个矛盾的论述,那么整个理论体系将无可救药。但一个没有矛盾的理论体系其掌控范围就受限。这就是希尔伯特提出第二个条件——完备性(completeness)的动机:他要求所有数学命题都可证明真伪。他的第三个条件是可判定性(decidability),要求有明确的机制程序确定任何数学命题的真假。希尔伯特在1930年的一次会议上宣称:“我们的口号是‘我们必须知道,我们终会知道’”。
仅仅一年后,哥德尔就给希尔伯特的梦想带来了第一次打击。他证明像“这个命题不可证”这样自相矛盾的论述可以从任意一组公理中推导出来。如果这样的命题确实无法被证明,那么这个理论就是不完整的,但如果它可以被证明,那么这个理论体系就是不一致的——更糟了。在同一篇论文中,哥德尔还证明,没有任何数学理论能证明其自身的一致性。
研究者们仍对未来的数学理论抱有希望,尽管它不一定完备,但仍可能是可判定的。也许他们可以开发一套程序,识别所有可证明的命题,就能避开像哥德尔这样恼人的命题。问题是没人知道怎么推理这些假设的程序。
1936年,图灵(Alan Turing)23岁,在读研究生。他用当时还不熟悉的计算机语言重新表述了希尔伯特的可判定性条件,并给了它致命一击。图灵创造了一个数学模型(现在叫图灵机),可以表示所有可能的算法,并表明,如果希尔伯特的程序存在,那么它将也适合这个模型。然后他借鉴哥德尔的自指方法证明,不可判定的程序——或者等价地,不可计算的问题是存在的,任何算法都不能解决。
希尔伯特的计划失败了:可证明和可计算的内容将永远存在基本限制。但随着计算机从抽象的理论演变成真实的机器,研究者们意识到,图灵将问题简单区分为可解决和不可解决,为后世留下许多未解之谜。到20世纪60年代,计算机科学家已经发展出解决某些问题的快速算法,但对于其他问题,唯一已知的算法慢得让人难以接受。如果问题不止是这些问题能否解决,还有这些问题解决起来有多困难呢?Carmosino 说:“丰富的理论出现了,但我们不再知道答案。”
不同的路径
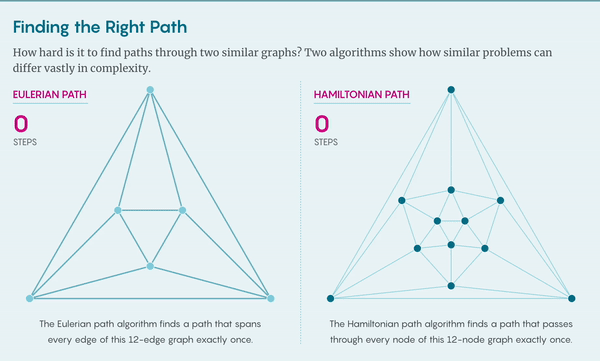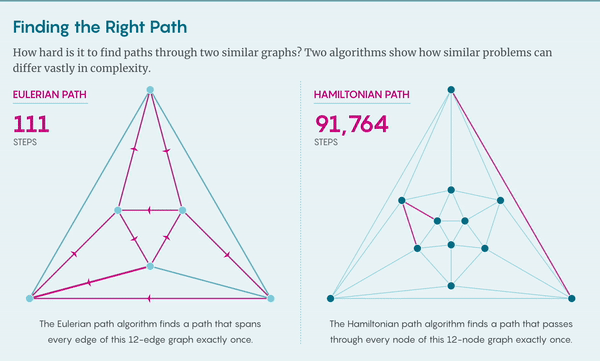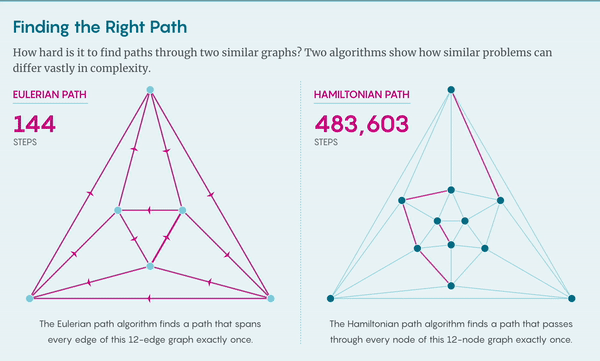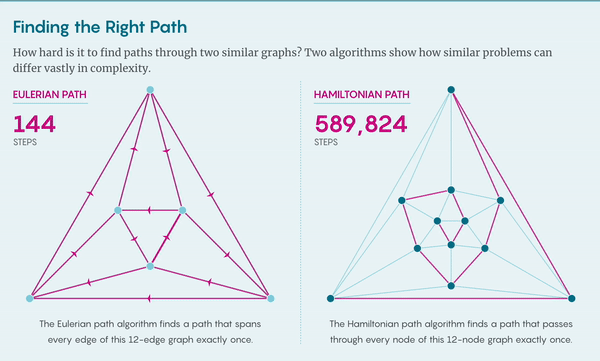
怎么形象地表示关于“难度”的问题如何让人头疼呢?让我们在图(graph)上讨论。节点(node)和连边(egde)组成网络,计算机科学家们用网络模拟从量子计算(quantum computation)到交通流等众多问题。
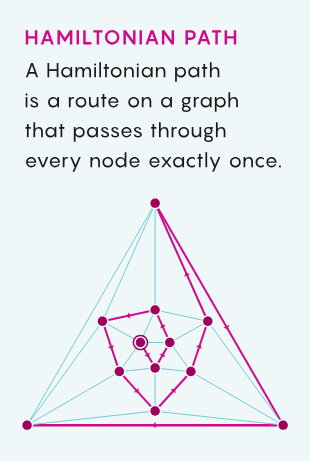
给你一个图,让你找到图上的哈密顿路径(Hamiltonian path,路径经过每个节点,且只经过一次)。这个问题理应是可以解决的,因为所有路径数量有限,即便别无他法,也可以检查每条路径是否符合要求。如果图上只有几个节点那就好办了,但对于稍微大一点的图,总路径数就会急剧上升以至失控,这个算法实际上就失效了。
还有更复杂的哈密顿路径算法,但算法解决问题所需的时间总是随着图的大小呈指数增长。加州大学圣迭戈分校(University of California, San Diego)的复杂性理论学家 Russell Impagliazzo 说:“图不需要特别大,但即使是最好的算法研究者也无法在 [任何合理的时间内] 找到路径,我说的 [合理的时间] 是指 [在宇宙终结之前]。”
哈密顿路径问题还有另一个有趣的性质。如果有人声称在特定图上找到了一条哈密顿路径,即使这个图非常大,你也可以快速地检查它的解是否正确。所需要做的仅是沿着路径逐一勾选节点,并检查确保没有勾选任何节点两次。如果最后没有节点丢失,那么这条路径就是哈密顿路径。
检查算法所需的时间与图的大小成正比,我们将其归入多项式算法类别,其运行时间随着图大小的多项式函数而增加。多项式增长比指数增长更温和,因此多项式算法即使在很大的图上也是可行的。Carmosino 说:“这大大提高了效率。”
哈密顿路径问题具有明显的不对称性(asymmetry):可以用多项式算法快速验证解,但求解则只能用缓慢的指数算法。这种不对称性也并不意外——欣赏艺术品总比创作更容易,验证数学定理总比证明要容易,但并非所有的计算问题都具有这样的不对称特征。事实上,有一个与寻找哈密顿路径非常相似的问题,其难度却截然不同。
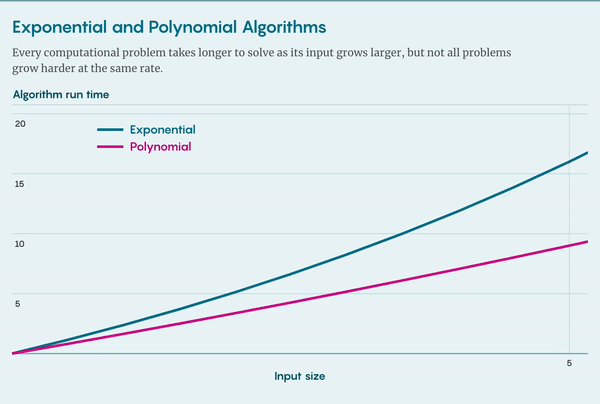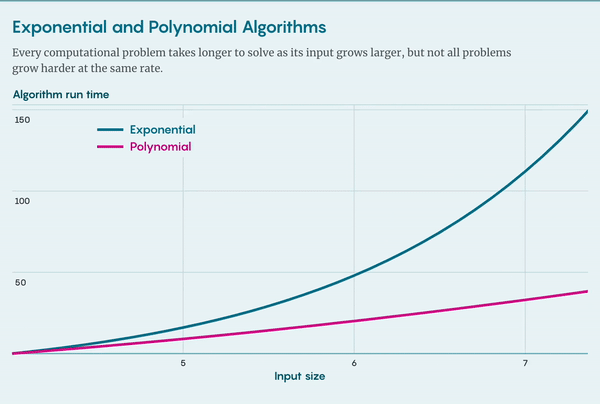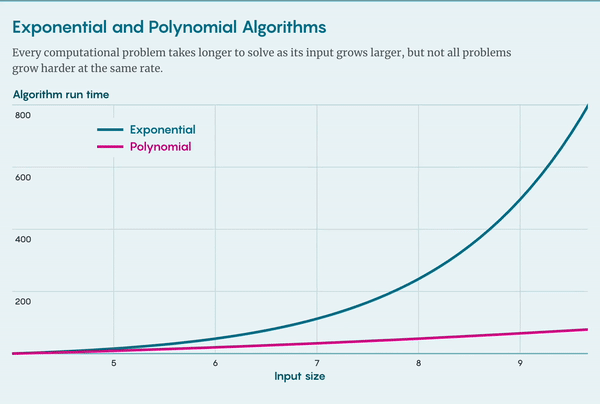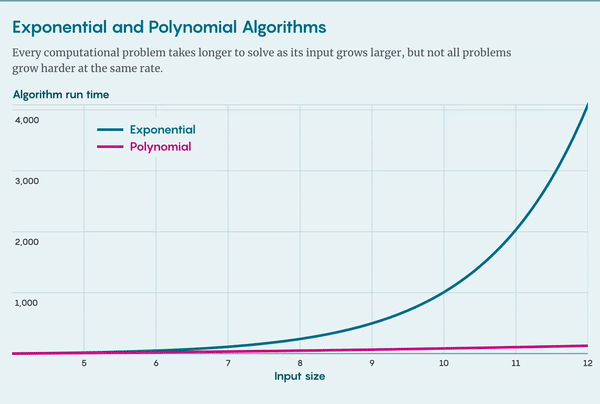
假设再给你一张图,现在要求你找到欧拉路径(Eulerian path),即经过每条边恰好一次的路径。同样的,可以用多项式算法验证解,但对于求解欧拉问题,也存在多项式算法,这个问题就不存在不对称。在复杂性理论中,某些路径似乎会比其他路径更好找。
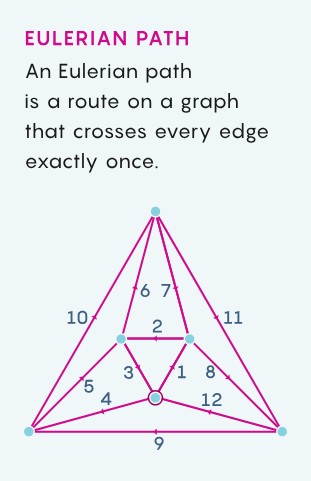
哈密顿路径问题和欧拉路径问题都属于复杂度类别 NP,NP 问题的定义是所有可以用多项式算法检验解的问题。欧拉路径问题也属于P类,因为可以用多项式算法求解。但显然,哈密顿路径问题不是这样的。为什么这两个图问题表面上如此相似,却有如此显著的不同?这就是P与NP问题的本质。
“普遍”问题
起初,复杂性类别似乎是为了分类出相似但不直接相关的问题——没有人怀疑过寻找哈密顿路径与其他困难计算问题之间有什么关系。直到1971年,复杂性理论学家 Stephen Cook 在美国获取终身教职受挫后,搬到多伦多大学,一年内就发表了一个非凡的结果。他发现了一个神奇的特定NP问题:如果存在一个多项式算法可以解决这个问题,那么它也可以解决NP中的其他所有问题。Cook 发现的这个“普遍”问题似乎是一根单独的柱子,支撑着看似困难问题的类别,将它们与地面的简单问题分开。一旦解决了这个问题,NP中的其余问题就会变得简单。
Cook 怀疑他的“普遍”问题没有快的算法,他在论文中也表达了这种怀疑,并补充道:“我觉得值得花费大量精力来证明这个猜想。”后来证明, “大量精力”的表述还是保守了。

大约在同时,苏联的本科生 Leonid Levin 证明了一个类似的结果,他确定了多个不同的普遍问题。此外,美国复杂性理论家 Richard Karp 证明,Cook 和 Levin 所确定的普遍性属性本身几乎普遍存在(尽管 Karp 和库克直到多年后才得知 Levin 的工作)。几乎所有没有已知多项式算法的NP问题,即几乎所有看似困难的容易验证的问题都具有相同的性质,这被称为NP完全问题(NP-completeness)。这意味着所有NP完全问题(包括哈密顿路径问题、数独和其他成千上万的问题)在精确意义上是等价的。“你面对的这些所有不同的问题,都神奇地变成了同一个问题,但我们仍不知道它是否能被解决。”Ilango说。
解决任何一个NP完全问题的难度足以媲美解决 P 和 NP 问题。如果P ≠ NP,则易于解决和难以解决的问题之间的差别就是遥不可及的天堑,被上千个柱子牢牢支撑;如果P = NP,那么整个结构就在崩溃的边缘摇摇欲坠,只等一块巨石落下。
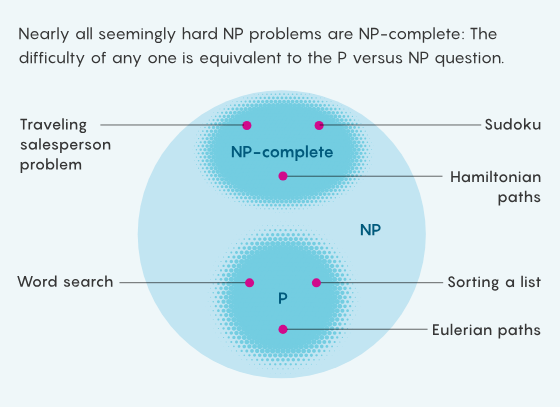
Cook、Levin 和 Karp 将这些看似不相关的问题统一了起来。现在,所有复杂性理论家都只需解决一个问题:P = NP吗?
五十年后,这个问题仍然没有答案。Kabanets 把关于计算能力极限的推理比作在一个广阔无垠的领域中进行勘测,只能看到一小部分,无法领略到全局。一个拥有无限计算能力的“神”却可以从山顶俯瞰,但凡人无法指望获得这种优势。“我们这些身处山脚下的人可以试着跳起来获得更好的视野,”Kabanets 说。
假设 P = NP。为了证明这一点,研究者们需要找到一个快速解决NP完全问题的算法,这个方法可能隐藏在广阔图景中的某个隐秘角落。没有人能保证很快可以找到它:复杂性理论家们或许只需要研究几十年,就能偶然发现一些解决看似困难(尽管不是NP完全)问题的巧妙算法。现在我们假设P ≠ NP。要证明这一点似乎更加困难。复杂性理论学家必须确定,不存在快速算法,才能有效地抢先挫败未来所有研究人员的努力。
有一部分问题在于不知从何入手。但是,这并不意味着研究者们没有尝试过。在过去几十年里,他们从许多角度探讨了这个问题,但均以失败告终。“这是计算机理论科学中最明显的事实之一,” Carmosino 说。“当一种现象如此持久时,就需要一些解释。”
2. 障碍
2. 障碍
到了 Carmosino 读大学的最后一年,好奇心引导他从哥德尔转向了复杂性理论的研究课程。他惊讶地发现,花在家庭作业上的时间比他最感兴趣的项目还要多,这个项目是一个计算机程序,可以学习童话故事的叙述结构并生成新的童话故事。“我想,我得认真对待这件事,” Carmosino 回忆说。不久之后,因为他对复杂性理论的研究过于投入,以至于导师温和地建议他重新考虑毕业后的计划。
“他说,‘你知道,如果你想继续做这个,如果你想继续研究计算机理论和复杂性理论,你可以去研究生院。’” Carmosino 说。获得硕士学位后,他在2012年搬到圣地亚哥,在 Impagliazzo 的指导下攻读博士学位。

起初,Carmosino 的主要目标是更好地理解20年前的一篇具有里程碑意义的论文,这篇论文激发了他的想象力。该论文由复杂性理论家 Alexander Razborov 和 Steven Rudich 撰写,证明 P ≠ NP 的“自然”策略肯定会失败,因为成功的代价将是加密技术的彻底崩溃,而研究人员认为这种情况非常不可能发生。研究人员将Razborov和Rudich的结果解释为证明 P ≠ NP 的流行方法的障碍。
“自然证明障碍”(natural proofs barrier)只是解决复杂性理论中开放问题已知的许多障碍之一。把这种障碍比作路障,就像在警告我们所有看似有希望的道路实际上都是一条死胡同。总之,这些障碍表明,任何解决P与NP问题的证明都必须与过去的证明方法截然不同;这就是为什么大多数研究者认为解决方案仍然遥不可及。但至少这些障碍可以告诉他们哪些地方不应该去尝试。Ilango表示:“复杂性理论的发展存在许多障碍,备受诅咒与祝福。”
当 Carmosino 遇到自然证明障碍时,它已经有将近20年的历史了。但他怀疑它能给研究者带来更多启发。这一天终会到来,他和三个同事从元复杂性的角度研究自然证明障碍,得到了一个令人惊讶的结果。他们的证明引发了人们对元复杂性(meta-complexity)的新兴趣,在之后几年里引发了一阵热潮。
要从自然证明障碍到元复杂性,我们必须回到20世纪70年代,那时的研究者们刚开始处理P与NP问题。是什么让证明问题变得如此困难?
电路复杂度
最初,研究人员试图证明 P ≠ NP —— 也就是说,证明存在一些 NP 问题 ,它们不能被任何可能的多项式算法所解决 —— 使用的是图灵用来证明一些问题根本无法被任何算法所解决的技巧的变体。但是他们很快发现了一个证明,表明这些方法是行不通的 —— 这是解决 P 和 NP 问题的第一个主要障碍。于是他们开始寻找另一种方法,很快就在图灵的同时代人香农(Claude Shannon)的工作中找到了一个。

Shannon 在北密歇根州的一个小镇长大,似乎不像是能开创信息时代的人物。然而,他证明了计算机科学这门新兴学科的跨学科性质。他对电气工程和数学逻辑都很熟悉。在他的硕士论文中,Shannon展示了由机电开关组成的电路如何表示包含布尔变量(只能取两个值,如0或1,真或假)的逻辑表达式。
在这些表达式中,布尔变量通过“逻辑门控”(logic gates)与(AND)、或(OR)和非(NOT)连接在一起。例如,初等表达式“A AND B”,当A和B都为真时为真,否则为假;另一方面,对于“A OR B”,如果A和B中至少有一个为真则为真。NOT 更简单:它可以反转单个变量的值。有了足够多的这些基本构件,就可以执行任何计算。
香农的工作为理论学家们提出了一种思考计算问题难度的新方法——“电路复杂度”(circuit complexity),尽管这里讨论的电路只是数学上的抽象。有一段时间,研究人员认为这种方法可以解决P与NP问题,但这条路最终还是遇到了自然证明障碍。

电路复杂度的框架要求研究者们重新思考图灵计算模型中最基本的概念。在这里,研究人员考虑的不是计算问题和解决这些问题的算法,而是布尔函数和计算它们的电路。布尔函数接受和输出布尔变量(0或1)。与算法一样,电路描述了在给定输入条件下产生输出的过程。“我的理解是,人们开始研究电路复杂度是因为他们认为图灵机太复杂了,”麻省理工学院的复杂性理论家 Ryan Williams 说。“我们可以一个门一个门地研究电路。”
所有的计算问题都可以有很多种算法,有些算法更快,许多不同的电路可以计算给定的任意布尔函数,有些电路的门数比其他电路更少。研究人员将电路复杂度定义为计算该函数的最小电路的总门数。对于一个输入变量固定的函数,电路复杂度也是固定的——某些函数的电路复杂度会高于其他函数。
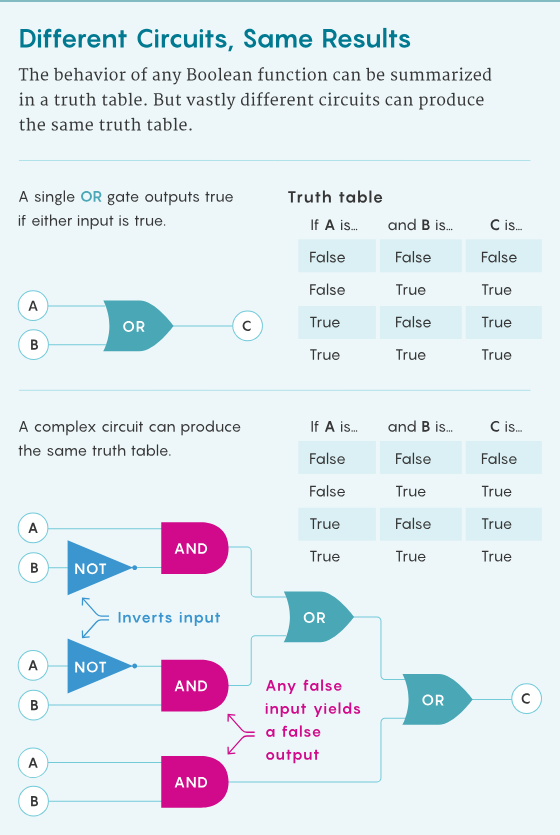
但在很多情况下,我们可以通过增加输入的变量数来考虑相同函数更复杂的版本,就像更大的图形会让寻找哈密顿路径更难一样。研究者们在研究算法运行时间时发问:计算布尔函数所需的最小门数是否随着输入变量数量的增加而呈多项式或指数增长?研究者们依据这个将函数划分成“易于计算”(多项式增长)和“难以计算”(指数增长)两类。
易于计算的布尔函数类似于P类计算问题,即可以在多项式时间内解决的问题。但是也存在类似于NP困难(NP-hard)问题的函数,研究人员发现计算这些函数的最佳方法随着门数量呈指数增长,但答案可以很容易地验证。如果复杂性理论家能够证明确实没有更好的方法能计算这样的函数,那么这就意味着P ≠ NP。
这是在20世纪80年代大多数复杂性理论学家追求的策略,而且他们占着上风。香农在1949年证明了几乎所有的布尔真值表(一个固定大小的布尔函数的所有可能输入和输出的长列表)都具有尽可能高的电路复杂度。他的论证非常简单:组合少量门的方法要比组合许多门的方法少得多。“我们没有那么多的小电路,”Aaronson说。
所以复杂性理论学家发现他们自己陷入了一个奇怪的困境。如果所有真值表都有很高的电路复杂度,那么几乎每个布尔函数都是很难计算的。研究人员只需要找到一个已知属于NP类并且具有高电路复杂度的布尔函数。这能有多难?
密码学与复杂性
起初,进展很快。1981年,Sipser和两个合作者证明,如果他们使用的电路对门的布置有一定的限制,那么,一个特定的布尔函数肯定是难以计算的。Sipser说:“我们当时幻想,可以证明这些受限模型的一些性质,然后基于所学知识来减少限制。”

1981年,Michael Sipser 用限制电路模型辅助证明了一个具有里程碑意义的结果,但最终陷入停滞。|来源:Bryce Vickmark
1985年,Razborov又迈出了一大步。当时他刚在莫斯科开始读研究生,在解决一个数学分支的问题时偶然加入了这项工作,结果发现解决这个问题的先决条件是P与NP问题。“我很幸运,当时我不知道这个问题有多难,”Razborov说。“否则也许我根本都不会开始。”
Razborov 分析了只包含AND和OR门的电路,并证明了无论门如何排列,这种电路都难以计算特定的NP完全的函数。所有研究人员要解决P与NP问题,就必须将 Razborov 的技术推广到带NOT门的电路中。Razborov说:“人们普遍认为,再多走两步,我们就会成功。”但事实并非如此。Razborov本人就证明了,如果把NOT门加入进来,他的方法就会失败,而且没有人能找到其他的方法。随着时间的流逝,他开始想,为什么这条路线会失效。
在美国,Ruzick 也在思考同样的问题。他和 Impagliazzo 是大学同学,又一起读研究生。他们的友谊源于对哥德尔和图灵自指论证的共同着迷,而且他们俩都对数学和计算机科学基础的影响感兴趣。“我们开玩笑说我们要得到一个标有‘自指’的按钮,”Impagliazzo说。

作为研究生,Rudich和Impagliazzo都在密码学的复杂性理论基础上工作,这一学科可能是试图证明P≠NP的最佳实践动机。密码学家通过“伪随机”来隐藏秘密信息——以这种方式加密的信息在任何窃听者看来都像是一堆随机的数字,但它仍然可以被预期的接收方解码。但是你怎么能确定一个想要窃听的人会发现破译密码太难了呢?
这是复杂性理论的战场。如今最广泛的加密方法都基于看似困难的NP问题。若要解密消息,攻击者就需要先发现能够快速解决NP问题的算法;若要证明加密方法的安全,我们就必须先证明P ≠ NP。“如果不能证明,那只能祈祷窃密者数学不好。”Sipser说。
虽然密码学本身很迷人,但它似乎与自指论证相差甚远,正是自指论证在最初吸引 Rudich 和 Impagliazzo 进入该领域。但随着 Rudich 努力理解为什么电路复杂度方法陷入停滞,他开始意识到这两个学科实际上并没有那么遥远。研究人员在尝试证明P ≠ NP时采取的策略具有自相矛盾的特征,让人想起了哥德尔的著名命题“这个陈述无法证明”,而密码学可以帮助解释原因。在俄罗斯,Razborov 在同一时间发现了类似的联系。这些是自然证明障碍的种子。
自然证明障碍的核心问题是,区分高复杂度函数和低复杂度函数的任务类似于区分用于加密信息的真正随机性和伪随机性。我们希望证明高复杂度函数与低复杂度函数有根本的区别,以证明P ≠ NP。但为了密码学的安全,我们也希望伪随机与真随机难以区分。也许我们不能两者兼得。
自然证明障碍
在1994年,Razborov 和 Rudich 意识到他们的发现如此相似!于是他们开始合作,将成果结合起来。他们首先发现,之前所有用电路复杂度来证明 P≠NP 的尝试都采用了相同的策略:识别一个NP完全布尔函数的特殊性质,然后证明任何一个容易计算的函数都没有这种性质。这表明选择的NP完全函数确实很难计算,从而证明P≠NP。
Sipser、Razborov等人用同样的策略成功地证明了他们更有限的结果,而且在每个案例中,研究人员发现的特殊属性是大多数布尔函数所共有的。因为没有已知的替代方法,Razborov 和 Rudich 甚至创造了“自然证据”这个词来指代这种性质共享的情况。如果“非自然”的证明是可能的,那么它必须是非常反直觉的,而且名副其实地“不自然”。
然后,Razborov 和 Rudich 证明了他们的主要结论:要想自然地证明 P≠NP,我们就需要全面地认识易于计算和难以计算函数之间的区别,而且这些知识还能够推动快速算法的发展,找出“隐藏的”易于计算的函数。如果复杂性理论家能够自然地证明P≠NP,他们就会发现一种几乎绝对正确的方法,只要看一眼任意真值表,就能确定相应的函数的电路复杂度是高还是低——这是一个比他们的目标更强、更普遍的结果。“你几乎无法阻挡意外之喜。”Carmosino 这样形容。
这就好像你试图核实一个具体的陈述,但每次尝试都变成了一个通用检验的蓝图——这看起来太好了,不像是真的。对于复杂性理论学家来说,自然证据的惊人力量同样使成功的可能性降低。但是,如果这样的证明成功了,由于电路复杂性和伪随机性之间的联系,对于密码学来说,可能是个坏消息。
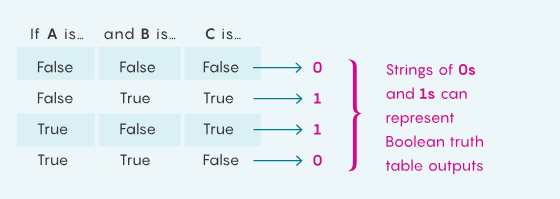
要理解这种联系,请想象一下,查看一个布尔函数的真值表的输出列,其中包含许多输入变量,并将每个“真”替换为1,每个“假”替换为0:
Merrill Sherman/Quanta Magazine
如果布尔函数具有较高的电路复杂度,那么这一长串输出在原则上与由0和1组成的真正随机字符串(比如通过反复抛硬币获得的字符串)是无法区分的。但如果函数的电路复杂度较低,那么貌似复杂的字符串也必须具有简单、简洁的描述。这使得它非常类似于密码学中使用的伪随机字符串,其简洁的描述是隐藏在明显的随机性中的秘密信息。

密码学中的真随机性和伪随机性。|来源:Merrill Sherman/Quanta Magazine
因此,Razborov 和 Rudich 的结果表明,任何 P≠NP 的自然证明产生的同时也会诞生一种快速算法,可以区分包含隐藏信息的伪随机字符串和真正的随机字符串。安全密码学是不可能的——这正好与研究人员希望通过证明 P≠NP 来建立的结果相反。
另一方面,如果安全密码学是可能的,那么自然证明就不能证明P≠NP——这是安全密码学的先决条件。简单地说,这就是自然证明障碍。复杂性理论似乎面临着一个残酷的笑话。“如果你相信复杂性,那么你就应该相信证明复杂性有多复杂,” Kabanets 说。
元复杂性
P≠NP 猜想的含义和证明它的困难之间的联系很有趣,但很难确定。一方面,自然证明障碍只阻止了一种证明P≠NP的方法。另一方面,它不把证明P≠NP的困难与P≠NP本身联系起来,而是与安全密码学联系起来。安全密码学与之密切相关但又不完全等同。为了真正理解这种联系,研究人员必须熟悉元复杂性(meta-complexity)。
Williams 说:“有一种直觉,‘哦,因为P≠NP,所以很难证明P≠NP’。但为了让这种直觉有意义,必须把证明 P≠NP 作为一个计算问题来考虑。”这就是 Kabanets 在研究生时期所做的。他在乌克兰长大,在苏联解体两年后完成了计算机科学的本科学业。但在随后的混乱中,他几乎没有机会研究自己最感兴趣的理论课题。

“我想做一些更学术的事情,”Kabanets回忆道。“我也好奇地想看看这个世界。”他搬到加拿大攻读研究生学位,在那里他了解了自然证明障碍。像 Carmosino 一样,Kabanets 被结果深深吸引:“这种联系似乎非常深刻。”2000年,他研究生快毕业时,在与复杂性理论学家蔡进一(Jin-Yi Cai)的谈话中,发现自然证明的障碍不断出现。蔡进一当时正在多伦多休假。他们开始把障碍视作邀请,这是一个精确研究证明困难问题到底有多难的机会。他们提出这一新观点的论文,成为新兴的元复杂性领域中最具影响力的早期作品之一。
论文题目:Circuit minimization problem
论文链接:https://dl.acm.org/doi/10.1145/335305.335314
Kabanets 和蔡进一的论文强调了 Razborov 和 Rudich 的自然证明障碍公式中隐含的一个计算问题:给定一个布尔函数的真值表,判断它的电路复杂度是高还是低。他们称之为最小电路尺寸问题(minimum circuit size problem),简称 MCSP。最小电路尺寸问题是一个典型的元复杂性问题:它是一个计算问题,但其主题不是图论或其他外部主题,而是复杂性理论本身。实际上,确实,这就像是驱使复杂性理论家们在20世纪80年代使用电路复杂性方法来解决P与NP问题的定量版本:哪些布尔函数难以计算,哪些则容易?Impagliazzo 说:“如果我们能够开发出一种解决最小电路尺寸问题的算法,那就像是在自动化我们在复杂性理论中所做的工作。它至少应该让我们对如何把工作做得更好有一个深刻的认识。”
复杂性理论家并不担心这种神奇的算法会让他们失去工作——因为他们认为它根本不存在,因为 Razborov 和 Rudich 表明,任何这种能区分高复杂度真值表和低复杂度真值表的算法都会毁灭密码学。这意味着MCSP可能是一个很难计算的问题。但这有多难呢?它是NP完全的吗,就像哈密顿路径问题和研究人员在20世纪60年代努力解决的几乎所有其他问题一样?
对于NP问题,“它有多难?”这个问题通常很容易回答,但最小电路尺寸问题(MCSP)很奇怪,似乎是例外。Kabanets 表示:“我们很少遇到与NP完全问题无关的‘真空’问题,尽管它们似乎很难解决。”
Kabanets 知道他和蔡进一并不是第一个考虑最小电路尺寸问题的人。苏联的数学家们早在20世纪50年代就研究过一个非常类似的问题,他们早期试图理解不同计算问题的内在难度。20世纪60年代后期,在发展NP完全理论的时候,Leonid Levin 曾与它斗争过,但他无法证明MCSP是NP完全的,于是他没有把MCSP放在他的重要论文里。
在那之后的30年里,这个问题几乎没有引起人们的注意,直到 Kabanets 和蔡进一注意到它与自然证明障碍的联系。Kabanets 并没有想要独自解决这个问题——相反,他想知道为什么要证明“这个看似困难的计算困难问题实际上是困难的”。“从某种意义上说,这是元元复杂性(meta-meta-complexity),”牛津大学的复杂性理论家Rahul Santhanam说。
但是,它是一直都很困难吗?还是至少有一些方法可以理解为什么研究人员没有成功证明最小电路尺寸问题(MCSP)是NP完全的?Kabanets 发现,是的,有一个原因:理解电路复杂性的困难就像一个障碍,阻碍了任何已知的策略来证明MCSP的NP完全性——这个问题本身是理解电路复杂性的困难。自然证明障碍扭曲的“自相矛盾”的逻辑似乎是不可避免的。也有可能最小电路尺寸问题(MCSP)不是NP完全的,但似乎也不太可能——因为我们已知某些更简单的变体问题是NP完全的。
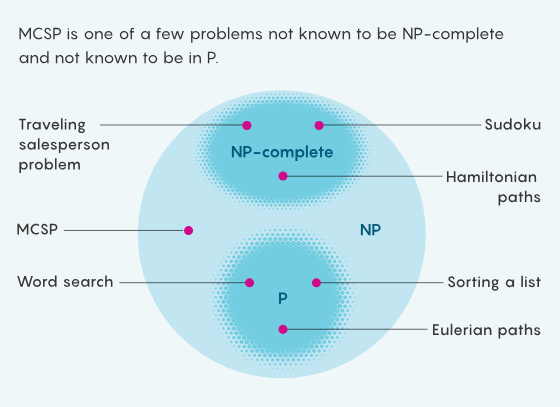
Impagliazzo 说:“我们只是不知道怎么把我们研究的所有问题联系起来。”
Kabanets 揭示了最小电路尺寸问题(MCSP)的奇怪行为,但他不知道接下来该怎么办。元复杂性的研究变得越来越少。16年后,当研究人员发现元复杂性与另一个基本问题的惊人联系时,这种想法再次蓬勃兴盛。这个问题是:如果你大多数时候只关心得到正确的答案,那么解决问题有多难?
复杂性的世界
对于日常问题,有通常有效的答案就很好了。例如,我们会根据日常的交通状况规划通勤,而非最坏的交通情况。
但大多数复杂性理论学家都难以满足:只有当他们找到对所有可能输入都能得到正确答案的快速算法时,才会声称一个问题很容易。这种标准方法根据研究人员所说的“最坏情况”的复杂性对问题进行分类。但也有一种“平均情况”(average-case)的复杂性理论,在这种理论中,如果有一个快速算法能在大多数情况下得到正确的答案,那么这个问题就是简单的。
对于密码学家来说,这种区别很重要。想象一个计算问题,算法能轻易解决几乎所有的情况,除了个别情况。最坏情况的复杂性理论认为这是一个困难的问题,但对于密码学来说这是无用的:如果只有很少的消息难以破译,那有什么意义呢?
事实上,在 Levin 关于NP完全理论的开创性工作发表十年后,他才开始对平均复杂度进行严格的研究。Levin 1978年移民到美国,在20世纪80年代中期,他开始关注平均复杂度。他开始与其他人合作,进一步发展这一理论,包括当时还在读研的 Impagliazzo。Impagliazzo 发现虽然研究者们在努力推进平均复杂性理论的发展,但他们经常偏离讨论的主题,没有直接针对问题进行讨论。他希望他们都对这个问题有相同的理解,尽管 Levin 的论文以简洁著称(开创平均复杂性领域的那篇论文不到两页长),但这也无济于事。
Leonid Levin 开创平均复杂性领域的论文
论文题目:Average Case Complete Problems
论文地址:https://epubs.siam.org/doi/10.1137/0215020
Impagliazzo说:“我本来打算把 Levin 的工作翻译成更易懂的文章。”他决定首先对大的图景做一个简短、有趣的概述,然后再深入讨论数学。“这几乎占满了当时的论文,而且也是人们唯一记得的部分。”该论文于1995年发表,立即成为经典之作。Impagliazzo 根据不同程度的计算难度和不同的密码学能力,将复杂性难度分为五类世界,并为它们创造了神奇的名字。我们生活在其中一个难度的世界,但不知道是哪一个。
论文题目:A personal view of average-case complexity
论文地址:https://ieeexplore.ieee.org/document/514853

自从 Impagliazzo 的论文发表以来,研究人员一直梦想着消除他的微型多重宇宙的一部分 ——通过证明某些世界根本不存在来缩小可能的空间。有两个世界特别引人注目,在其中,即使 P ≠ NP,当前的加密算法也无法实现安全的加密通信。
在其中一个被称为 Heuristica 的世界中,所有NP完全问题在大多数输入上都是容易解决的,但快速算法偶尔会出现错误,因此按照最坏情况复杂性理论的标准,这些问题仍然被认为是困难的。因为在这个世界中几乎所有的代码都很容易被破解,因此加密是不可能的。在另一个名为 Pessiland 的世界中,加密之所以不可能是另一个原因:每个问题在平均情况下都是困难的,但加密一条消息会让它的目标接收者也无法理解。
这两个世界与元复杂性问题密切相关——特别是 Heuristica 的命运与最小电路尺寸问题(MCSP)是否是NP完全的问题有关。Kabanets 和 Levin 多年前所着迷的问题不仅仅是出于好奇:有一个完整的世界岌岌可危。为了排除掉 Heuristica,研究者们必须消除最坏情况和平均情况之间的区别,也就是说,他们必须证明任何假设的算法都可以在大多数情况下正确解决NP完全问题,并且可以在所有情况下实际解决问题。这种联系称为最坏情况到平均情况的约简(worst-case to average-case reduction),虽然已经证明对于某些问题,这种约简是存在的,但这些问题都不是NP完全的,因此这些结果并不会给出更多的信息。如果能够证明 Heuristica 不存在,那么在 P ≠ NP 的情况下实现安全的加密通信就更容易了。
但要排除掉 Heuristica 并不容易。2003年,两位复杂性理论家表明,证明已知NP完全问题的最坏情况到平均情况的约简的现有方法将导致荒谬的后果,这表明这样的证明可能行不通。研究人员必须找到另一种方法,现在他们认为最小电路尺寸问题(MCSP)可能正是他们需要的问题。但这在十多年后才变得清晰起来。Carmosino 对自然证明障碍的执着追求,让我们第一次看到了这种联系。
论文题目:On worst-case to average-case reductions for NP problems
论文地址:https://ieeexplore.ieee.org/document/1238205
3. 机遇
3. 机遇
通过 Kabanets 和其他四名研究人员于2013年发表的一篇论文,Carmosino 在研究生期间首次接触到元复杂性研究,该论文进一步发展了 Kabanets 十多年前开创的自然证明障碍的方法。这让他更加相信,我们仍然可以从 Razborov 和 Rudich 的经典论文中学到很多东西。
论文题目:Mining Circuit Lower Bound Proofs for Meta-Algorithms
论文地址:https://eccc.weizmann.ac.il/report/2013/057/
“当时我沉迷于那篇论文,”Carmosino 说。“一切都没有改变。”在访问加州大学伯克利分校长达一学期的研讨会时,他的痴迷终于结出果实。在那里,他花了很多时间与 Impagliazzo、Kabanets 和 Antonina Kolokolova 交谈,Antonina Kolokolova 是纽芬兰纪念大学的复杂性理论家,曾与 Kabanets 合作撰写2013年的论文。Carmosino 之前曾与他们三人合作过,这种成功的合作给了他信心,他能够向这三个人提出关于这个主题的最迷人问题。
“他以一种好的方式困扰着人们,”Kabanets 回忆道。起初,Carmosino 为证明 Razborov 和 Rudich 论文中自然证明障碍的最小电路尺寸问题(MCSP)版本具有NP完全性提出了新的想法,但这些想法并没有奏效。相反,Impagliazzo 不经意间的评论使这四名研究人员意识到,自然证明障碍可以产生比任何人想象的更强大的算法——在自然证明障碍中存在一个秘密地图。

在2016年的一篇文章中,这四名研究人员证明,某种平均情况下的MCSP算法可以用来构建一种最坏情况下的算法,用于识别隐藏在随机数字串中的模式——计算机科学家将此任务称为“学习”。这是一个惊人的结果,因为从直观上看,学习似乎比MCSP算法执行的二元分类任务(复杂性高还是低)更难。而且令人惊讶的是,它将一个任务的最坏情况复杂性与另一个任务的平均情况复杂性联系起来。
论文题目:Learning algorithms from natural proofs
论文地址:https://dl.acm.org/doi/10.5555/2982445.2982455
“这种联系是否存在并不明显,”Impagliazzo说。对于一般的布尔电路,MCSP的快速算法纯属假设:除非我们能证明MCSP是一个容易计算的问题,否则这种快速算法根本不可能存在,而这意味着这四名研究人员论文中暗示的学习算法也是同样假设的。
但是对于一些更简单的MCSP版本——当电路具有特定限制时,区分复杂度高和低的真值表,早在很多年前就已经有了快速算法。Carmosino、Impagliazzo、Kabanets 和 Kolokolova的论文表明,这些算法可以转化为同样受到限制的“学习”算法。尽管这些算法受到限制,但它们仍然比研究人员此前在严格理论水平上所理解的任何算法都要强大。“不知为何,他们的‘自指’能让你做一些似乎在更标准的问题上做不到的事情。”Ilango说。这一结果引起了其他主题的复杂性理论家的关注。这也是在之后几年,元复杂性和平均情况复杂性之间出现进一步联系的预兆。最重要的是,这证明了研究人员可以通过问一些简单的问题来取得大的进步,虽然这些问题一开始似乎只会阻碍他们的进步。Impagliazzo 说:“这种对偶性(duality)贯穿了过去至少30或40年的复杂性研究。机遇与挑战往往并存。”
部分问题的证明
自从 Carmosino 和他的同事发表了论文之后,进展才得以加速。Kolokolova 说:“复杂性研究的进展日新月异,现在有很多非常非常聪明的年轻人加入。”
Ilango 就是这群年轻人之一,在读研的前三年内,他采用双管齐下的策略,证明了“MCSP问题是NP完全的”这样艰巨的开放问题:正如电路复杂性研究者在上世纪80年代挑战 P 和 NP 问题时那样,在证明MCSP更简单版本NP完全的同时,也证明了 MCSP 更复杂版本的 NP 完全性。证明复杂版本的 MCSP 的NP完全性在直觉上似乎更难,因此要证明它更困难就更容易。Ilango 将他对元复杂性的兴趣归功于 Eric Allender,他是罗格斯大学的复杂性理论家,是少数在2000年代和2010年代初继续研究元复杂性的研究人员之一。“他的热情很有感染力,” Ilango说。
另一位受 Allender 启发的年轻研究员是 Shuichi Hirahara,目前是东京国家信息研究所(National Institute of Informatics)的教授。2018年,当Hirahara还是一名研究生时,他揭示了 Carmosino 和他的合作者发现的元复杂性与平均复杂性之间的本质关系。这四名研究人员发现了一个问题:MCSP的平均复杂性与布尔学习问题的最坏情况复杂性之间的联系。Hirahara 进一步发展了他们的技术,推导出MCSP的最坏情况到平均情况的约简。他的结果表明,像 Carmosino 和他的同事考虑的那种假设的平均情况 MCSP 算法实际上足够强大,即使 MCSP 问题稍有不同,该算法仍然能够成功地解决问题,而且不会犯错。

Hirahara的结果令人兴奋,因为许多研究人员怀疑MCSP是NP完全的,与其他所有已知最坏情况到平均情况的约简问题不同。如果他们能够将 Hirahara 的结果扩展到所有平均情况算法,并证明MCSP是NP完全的,那么这将证明前面谈论的 Heuristica 世界将坍塌。“那真的会是一个震撼人心的结果,”Santhanam 说。证明MCSP是NP完全的可能是一个艰巨的任务。毕竟,这个问题已经公开了50多年。但是在去年 Hirahara 取得了突破之后,研究人员现在离目标更近了,比几年前任何人的预期都要近。
Hirahara 证明了部分MCSP问题(MCSP问题的一个变体)的NP完全性,这个问题忽略了每个真值表中的某些项。他的证明建立在 Ilango 开发的方法上,该方法表明部分MCSP(partial MCSP)问题等价于一个看似无关的问题。这个问题涉及一种名为秘密共享的加密技术,这是一种将加密信息分配给许多人的方法,只有在他们中的某些人合作时,信息才能被解码。
对于任何实际的密码学应用,你都希望事先知道需要多少人进行合作,但是在额外的密码学技巧的帮助下,可以构造一个令人沮丧的场景,在其中我们甚至很难知道需要多少人合作。Hirahara 找到了一种方法来证明如此设计的密码问题是NP完全的,并且表明该证明暗示了部分MCSP的NP完全性。
这个结果给元复杂性研究人员带来的鼓励甚至超过了 Hirahara 早期的工作,其他研究人员也注意到了这一点——复杂性理论家 Lance Fortnow 称其为年度成果。这是因为处理这样的“部分函数”版本的计算问题一直是其他NP完全证明的关键中间步骤。“这是一项了不起的工作,”Williams 说。“每个人都认为,这种“部分问题”与完整问题的难度大致相同。”
证明完整的 MCSP 的NP完全问题仍然面临障碍。但这些障碍并不需要我们找到新的工具包,可能通过已知技术的正确整合就能解决这个障碍。这一证明将最终解决自复杂性理论存在以来阻碍分类的少数几个问题之一。Levin 在邮件中谦虚地写道:“我没能看到它,我实在是太笨了:-)。”
缺失的碎片
MCSP甚至不是唯一引发重大突破的元复杂性问题。2020年,康奈尔科技校区的密码学家 Rafael Pass 和他的研究生 Yanyi Liu 发现了一个不同的元复杂性问题,而且他们还定义了 Heuristica 和 Pessiland 之间边界的基本密码学协议之间的联系。Pessiland 是 Impagliazzo 提出的五个世界中最糟糕的一个(NP 完全问题在平均情况下难以解决,但密码学仍然不安全)。他们研究的问题是消灭 Pessiland 的主力军,他们最近的工作表明,它也可以消灭 Heuristica。
Pass 说:“拼图有不同碎片缺失了,但对我来说,这些领域的联系如此紧密实在是太神奇了!”Hirahara 警告说,对于那些试图消灭 Impagliazzo 在30年前构想的部分世界的研究者们来说,前方仍有挑战。“但我想说的是,某天我们一定能够排除掉 Heuristica 和 Pessiland,只是我不知道这一天什么时候到来。”
许多研究人员预计,最大的困难将是弥合两种不同平均复杂性模型之间看似无害的差距。密码学家通常研究在两个方向上都会犯错误的平均情况算法,偶尔会将随机字符串错误地标记为伪随机,反之亦然。与此同时,Hirahara 从最坏情况到平均情况的约简适用于只犯第一种类型错误的平均情况算法。像这样的微妙区别可能会在复杂性理论中产生重大影响。但是,尽管存在这个障碍和其他许多问题,Allender 仍不禁表现出谨慎的乐观情绪。Allender 说:“我尽量不让自己报有过高的期望,因为以往的记录表明,很多进展是无用的。但我们看到了很多令人兴奋的进展——克服看似障碍的方法。”
如果要问研究者们在与“P与NP”问题(the P versus NP question)的斗争中学到了什么?或者说从中理解了什么,那一定是复杂性理论本身是复杂的。但也正是这个挑战让探索变得如此有意义。Carmosino 说:“这个问题真的很难,这一点实在是太棒了,我将永不厌倦!”
AI By Complexity读书会招募中
大模型、多模态、多智能体层出不穷,各种各样的神经网络变体在AI大舞台各显身手。复杂系统领域对于涌现、层级、鲁棒性、非线性、演化等问题的探索也在持续推进。而优秀的AI系统、创新性的神经网络,往往在一定程度上具备优秀复杂系统的特征。因此,发展中的复杂系统理论方法如何指导未来AI的设计,正在成为备受关注的问题。
集智俱乐部联合加利福尼亚大学圣迭戈分校助理教授尤亦庄、北京师范大学副教授刘宇、北京师范大学系统科学学院在读博士张章、牟牧云和在读硕士杨明哲、清华大学在读博士田洋共同发起「AI By Complexity」读书会,探究如何度量复杂系统的“好坏”?如何理解复杂系统的机制?这些理解是否可以启发我们设计更好的AI模型?在本质上帮助我们设计更好的AI系统。读书会于6月10日开始,每周一晚上20:00-22:00举办。欢迎从事相关领域研究、对AI+Complexity感兴趣的朋友们报名读书会交流!
点击“阅读原文”,报名读书会










